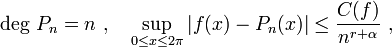Bernstein's theorem (approximation theory)

In approximation theory, Bernstein's theorem is a converse to Jackson's theorem.[1] The first results of this type were proved by Sergei Bernstein in 1912.[2]

For approximation by trigonometric polynomials, the result is as follows:

Let f: [0, 2π] → C be a 2π-periodic function, and assume r is a natural number, and 0 < α < 1. If there exists a number C(f) > 0 and a sequence of trigonometric polynomials {Pn}n ≥ n0 such that

\deg\, P_n = n~, \quad \sup_{0 \leq x \leq 2\pi} |f(x) - P_n(x)| \leq \frac{C(f)}{n^{r + \alpha}}~,

then f = Pn0 + φ, where φ has a bounded r-th derivative which is α-Hölder continuous.

See also

References

  1. ↑ Achieser, N.I. (1956). Theory of Approximation. New York: Frederick Ungar Publishing Co.
  2. ↑ Bernstein, S.N. (1952). Collected works, 1. Moscow. pp. 11–104.