Bernoulli distribution
| Parameters |
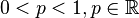 |
|---|---|
| Support |
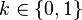 |
| pmf |
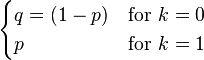 |
| CDF |
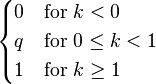 |
| Mean |
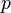 |
| Median |
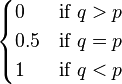 |
| Mode |
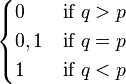 |
| Variance |
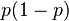 |
| Skewness |
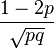 |
| Ex. kurtosis |
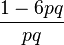 |
| Entropy |
 |
| MGF |
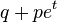 |
| CF |
 |
| PGF |
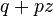 |
| Fisher information |
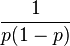 |
In probability theory and statistics, the Bernoulli distribution, named after Swiss scientist Jacob Bernoulli, is the probability distribution of a random variable which takes value 1 with success probability  and value 0 with failure probability
and value 0 with failure probability 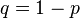 . It can be used, for example, to represent the toss of a coin, where "1" is defined to mean "heads" and "0" is defined to mean "tails" (or vice versa).
. It can be used, for example, to represent the toss of a coin, where "1" is defined to mean "heads" and "0" is defined to mean "tails" (or vice versa).
Properties
If  is a random variable with this distribution, we have:
is a random variable with this distribution, we have:
A classical example of a Bernoulli experiment is a single toss of a coin. The coin might come up heads with probability  and tails with probability
and tails with probability  . The experiment is called fair if
. The experiment is called fair if 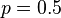 , indicating the origin of the terminology in betting (the bet is fair if both possible outcomes have the same probability).
, indicating the origin of the terminology in betting (the bet is fair if both possible outcomes have the same probability).
The probability mass function  of this distribution is
of this distribution is
This can also be expressed as
The expected value of a Bernoulli random variable  is
is
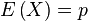
and its variance is
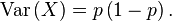
Bernoulli distribution is a special case of the Binomial distribution with 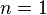 .[1]
.[1]
The kurtosis goes to infinity for high and low values of  , but for
, but for 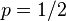 the Bernoulli distribution has a lower excess kurtosis than any other probability distribution, namely −2.
the Bernoulli distribution has a lower excess kurtosis than any other probability distribution, namely −2.
The Bernoulli distributions for 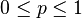 form an exponential family.
form an exponential family.
The maximum likelihood estimator of  based on a random sample is the sample mean.
based on a random sample is the sample mean.
Related distributions
- If
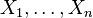 are independent, identically distributed (i.i.d.) random variables, all Bernoulli distributed with success probability p, then
are independent, identically distributed (i.i.d.) random variables, all Bernoulli distributed with success probability p, then
The Bernoulli distribution is simply 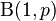 .
.
- The categorical distribution is the generalization of the Bernoulli distribution for variables with any constant number of discrete values.
- The Beta distribution is the conjugate prior of the Bernoulli distribution.
- The geometric distribution models the number of independent and identical Bernoulli trials needed to get one success.
- If Y ~ Bernoulli(0.5), then (2Y-1) has a Rademacher distribution.
See also
Notes
- ↑ McCullagh and Nelder (1989), Section 4.2.2.
References
- McCullagh, Peter; Nelder, John (1989). Generalized Linear Models, Second Edition. Boca Raton: Chapman and Hall/CRC. ISBN 0-412-31760-5.
- Johnson, N.L., Kotz, S., Kemp A. (1993) Univariate Discrete Distributions (2nd Edition). Wiley. ISBN 0-471-54897-9
External links
- Hazewinkel, Michiel, ed. (2001), "Binomial distribution", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Weisstein, Eric W., "Bernoulli Distribution", MathWorld.
- Interactive graphic: Univariate Distribution Relationships
| ||||||||||||||
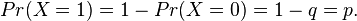
![f(k;p) = \begin{cases} p & \text{if }k=1, \\[6pt]
1-p & \text {if }k=0.\end{cases}](../I/m/4a24eb0c61b03cb0b1865292e8d3c846.png)
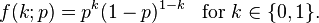
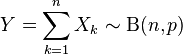 (
(