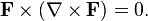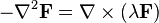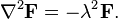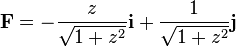Beltrami vector field

In vector calculus, a Beltrami vector field, named after Eugenio Beltrami, is a vector field in three dimensions that is parallel to its own curl. That is, F is a Beltrami vector field provided that

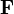\mathbf{F}\times (\nabla\times\mathbf{F})=0.

If \mathbf{F} is solenoidal - that is, if 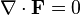\nabla \cdot \mathbf{F} = 0 such as for an incompressible fluid or a magnetic field, we may examine 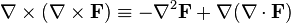\nabla \times (\nabla \times \mathbf{F}) \equiv -\nabla^2 \mathbf{F} + \nabla (\nabla \cdot \mathbf{F}) and apply this identity twice to find that

-\nabla^2 \mathbf{F} = \nabla \times(\lambda \mathbf{F})

and if we further assume that \lambda is a constant, we arrive at the simple form

\nabla^2 \mathbf{F} = -\lambda^2 \mathbf{F}.

Beltrami vector fields with nonzero curl correspond to Euclidean contact forms in three dimensions.

The vector field

\mathbf{F} = -\frac{z}{\sqrt{1+z^2}}\mathbf{i} + \frac{1}{\sqrt{1+z^2}}\mathbf{j}

is a multiple of the standard contact structure −z i + j, and furnishes an example of a Beltrami vector field.

See also

References