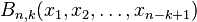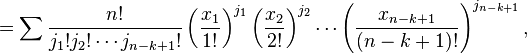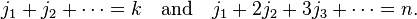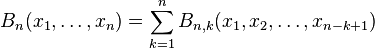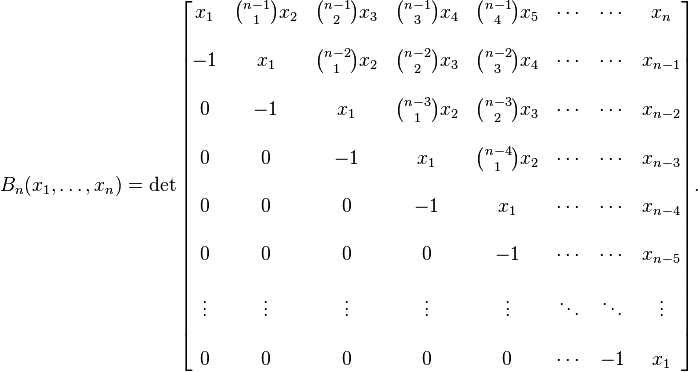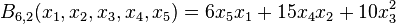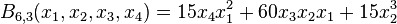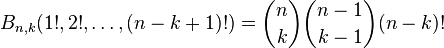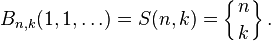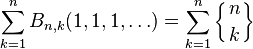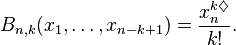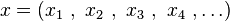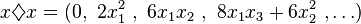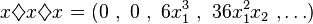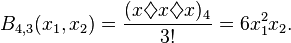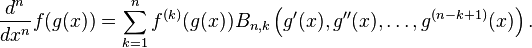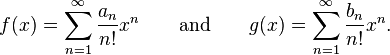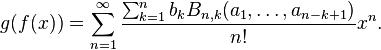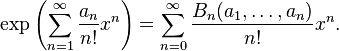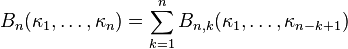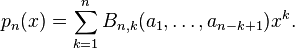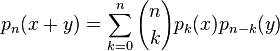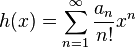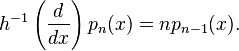Bell polynomials

In combinatorial mathematics, the Bell polynomials, named in honor of Eric Temple Bell, are a triangular array of polynomials given by

B_{n,k}(x_1,x_2,\dots,x_{n-k+1})

=\sum{n! \over j_1!j_2!\cdots j_{n-k+1}!} \left({x_1\over 1!}\right)^{j_1}\left({x_2\over 2!}\right)^{j_2}\cdots\left({x_{n-k+1} \over (n-k+1)!}\right)^{j_{n-k+1}},

where the sum is taken over all sequences j₁, j₂, j₃, ..., j_n−k+1 of non-negative integers such that

j_1+j_2+\cdots = k\quad\mbox{and}\quad j_1+2j_2+3j_3+\cdots=n.

Complete Bell polynomials

The sum

B_n(x_1,\dots,x_n)=\sum_{k=1}^n B_{n,k}(x_1,x_2,\dots,x_{n-k+1})

is sometimes called the nth complete Bell polynomial. In order to contrast them with complete Bell polynomials, the polynomials B_n, k defined above are sometimes called "partial" Bell polynomials.

The complete Bell polynomials satisfy the following identity

B_n(x_1,\dots,x_n) = \det\begin{bmatrix}x_1 & {n-1 \choose 1} x_2 & {n-1 \choose 2}x_3 & {n-1 \choose 3} x_4 & {n-1 \choose 4} x_5 & \cdots & \cdots & x_n \\ \\ -1 & x_1 & {n-2 \choose 1} x_2 & {n-2 \choose 2} x_3 & {n-2 \choose 3} x_4 & \cdots & \cdots & x_{n-1} \\ \\ 0 & -1 & x_1 & {n-3 \choose 1} x_2 & {n-3 \choose 2} x_3 & \cdots & \cdots & x_{n-2} \\ \\ 0 & 0 & -1 & x_1 & {n-4 \choose 1} x_2 & \cdots & \cdots & x_{n-3} \\ \\ 0 & 0 & 0 & -1 & x_1 & \cdots & \cdots & x_{n-4} \\ \\ 0 & 0 & 0 & 0 & -1 & \cdots & \cdots & x_{n-5} \\ \\ \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \ddots & \vdots \\ \\ 0 & 0 & 0 & 0 & 0 & \cdots & -1 & x_1 \end{bmatrix}.

Combinatorial meaning

If the integer n is partitioned into a sum in which "1" appears j₁ times, "2" appears j₂ times, and so on, then the number of partitions of a set of size n that collapse to that partition of the integer n when the members of the set become indistinguishable is the corresponding coefficient in the polynomial.

Examples

For example, we have

B_{6,2}(x_1,x_2,x_3,x_4,x_5)=6x_5x_1+15x_4x_2+10x_3^2

because there are

6 ways to partition a set of 6 as 5 + 1,

15 ways to partition a set of 6 as 4 + 2, and

10 ways to partition a set of 6 as 3 + 3.

Similarly,

B_{6,3}(x_1,x_2,x_3,x_4)=15x_4x_1^2+60x_3x_2x_1+15x_2^3

because there are

15 ways to partition a set of 6 as 4 + 1 + 1,

60 ways to partition a set of 6 as 3 + 2 + 1, and

15 ways to partition a set of 6 as 2 + 2 + 2.

Properties

$B_{n,k}(1!,2!,\dots,(n-k+1)!) = \binom{n}{k}\binom{n-1}{k-1} (n-k)!$

Stirling numbers and Bell numbers

The value of the Bell polynomial B_n,k(x₁,x₂,...) when all xs are equal to 1 is a Stirling number of the second kind:

B_{n,k}(1,1,\dots)=S(n,k)=\left\{{n\atop k}\right\}.

The sum

\sum_{k=1}^n B_{n,k}(1,1,1,\dots) = \sum_{k=1}^n \left\{{n\atop k}\right\}

is the nth Bell number, which is the number of partitions of a set of size n.

Convolution identity

For sequences x_n, y_n, n = 1, 2, ..., define a sort of convolution by:

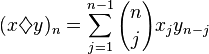(x \diamondsuit y)_n = \sum_{j=1}^{n-1} {n \choose j} x_j y_{n-j}

Note that the bounds of summation are 1 and n − 1, not 0 and n .

Let 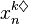$x_n^{k\diamondsuit}\,$ be the nth term of the sequence

\displaystyle\underbrace{x\diamondsuit\cdots\diamondsuit x}_{k\ \mathrm{factors}}.\,

Then

B_{n,k}(x_1,\dots,x_{n-k+1}) = {x_{n}^{k\diamondsuit} \over k!}.\,

For example, let us compute 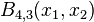$B_{4,3}(x_1,x_2)$ . We have

x = ( x_1 \ , \ x_2 \ , \ x_3 \ , \ x_4 \ , \dots )

x \diamondsuit x = ( 0,\ 2 x_1^2 \ ,\ 6 x_1 x_2 \ , \ 8 x_1 x_3 + 6 x_2^2 \ , \dots )

x \diamondsuit x \diamondsuit x = ( 0 \ ,\ 0 \ , \ 6 x_1^3 \ , \ 36 x_1^2 x_2 \ , \dots )

and thus,

B_{4,3}(x_1,x_2) = \frac{ ( x \diamondsuit x \diamondsuit x)_4 }{3!} = 6 x_1^2 x_2.

Applications of Bell polynomials

Faà di Bruno's formula

Main article: Faà di Bruno's formula

Faà di Bruno's formula may be stated in terms of Bell polynomials as follows:

{d^n \over dx^n} f(g(x)) = \sum_{k=1}^n f^{(k)}(g(x)) B_{n,k}\left(g'(x),g''(x),\dots,g^{(n-k+1)}(x)\right).

Similarly, a power-series version of Faà di Bruno's formula may be stated using Bell polynomials as follows. Suppose

f(x)=\sum_{n=1}^\infty {a_n \over n!} x^n \qquad \mathrm{and} \qquad g(x)=\sum_{n=1}^\infty {b_n \over n!} x^n.

Then

g(f(x)) = \sum_{n=1}^\infty {\sum_{k=1}^{n} b_k B_{n,k}(a_1,\dots,a_{n-k+1}) \over n!} x^n.

In particular, the complete Bell polynomials appear in the exponential of a formal power series:

\exp\left(\sum_{n=1}^\infty {a_n \over n!} x^n \right) = \sum_{n=0}^\infty {B_n(a_1,\dots,a_n) \over n!} x^n.

Moments and cumulants

The sum

B_n(\kappa_1,\dots,\kappa_n)=\sum_{k=1}^n B_{n,k}(\kappa_1,\dots,\kappa_{n-k+1})

is the nth moment of a probability distribution whose first n cumulants are κ₁, ..., κ_n. In other words, the nth moment is the nth complete Bell polynomial evaluated at the first n cumulants.

Representation of polynomial sequences of binomial type

For any sequence a₁, a₂, a₃, ... of scalars, let

p_n(x)=\sum_{k=1}^n B_{n,k}(a_1,\dots,a_{n-k+1}) x^k.

Then this polynomial sequence is of binomial type, i.e. it satisfies the binomial identity

p_n(x+y)=\sum_{k=0}^n {n \choose k} p_k(x) p_{n-k}(y)

for n ≥ 0. In fact we have this result:

Theorem: All polynomial sequences of binomial type are of this form.

If we let

h(x)=\sum_{n=1}^\infty {a_n \over n!} x^n

taking this power series to be purely formal, then for all n,

h^{-1}\left( {d \over dx}\right) p_n(x) = n p_{n-1}(x).

Software

Bell polynomials, complete Bell polynomials and generalized Bell polynomials are implemented in Mathematica as BellY, in Maple as BellB, and in Sage as bell_polynomial.

References

Eric Temple Bell (1927–1928). "Partition Polynomials". Annals of Mathematics 29 (1/4): 38–46. doi:10.2307/1967979. JSTOR 1967979. MR 1502817.
Louis Comtet (1974). Advanced Combinatorics: The Art of Finite and Infinite Expansions. Dordrecht, Holland / Boston, U.S.: Reidel Publishing Company.
Steven Roman. The Umbral Calculus. Dover Publications.
Vassily G. Voinov, Mikhail S. Nikulin (1994). "On power series, Bell polynomials, Hardy-Ramanujan-Rademacher problem and its statistical applications". Kybernetika 30 (3): 343–358. ISSN 0023-5954.
Andrews, George E. (1998). The Theory of Partitions. Cambridge Mathematical Library (1st pbk ed.). Cambridge University Press. pp. 204–211. ISBN 0-521-63766-X.
Silvia Noschese, Paolo E. Ricci (2003). "Differentiation of Multivariable Composite Functions and Bell Polynomials". Journal of Computational Analysis and Applications 5 (3): 333–340. doi:10.1023/A:1023227705558.
Abbas, Moncef; Bouroubi, Sadek (2005). "On new identities for Bell's polynomial". Disc. Math (293): 5–10. doi:10.1016/j.disc.2004.08.023. MR 2136048.
Khristo N. Boyadzhiev (2009). "Exponential Polynomials, Stirling Numbers, and Evaluation of Some Gamma Integrals". Abstract and Applied Analysis 2009: Article ID 168672. doi:10.1155/2009/168672. (contains also elementary review of the concept Bell-polynomials)
V. V. Kruchinin (2011). "Derivation of Bell Polynomials of the Second Kind". arXiv:1104.5065.
Griffiths, Martin (2012). "Families of sequences from a class of multinomial sums". Journal of Integer Sequences 15. MR 2872465.

Bell polynomials

Complete Bell polynomials

Combinatorial meaning

Examples

Properties

Stirling numbers and Bell numbers

Convolution identity

Applications of Bell polynomials

Faà di Bruno's formula

Moments and cumulants

Representation of polynomial sequences of binomial type

Software

See also

References