Behavioral momentum
Behavioral momentum is a theory in quantitative analysis of behavior and is a comparative metaphor based on physical momentum. It describes the general relation between resistance to change (persistence of behavior) and the rate of reinforcement obtained in a given situation.
B.F. Skinner (1938) proposed that all behavior is based on the fundamental unit of behavior termed the discriminated operant. The discriminated operant, also known as the three-term contingency, is broken down into three necessary components: an antecedent discriminative-stimulus context, a response, and a reinforcing or punishing consequence. Responding occurs in the presence of the stimulus because responding previously has resulted in a consequence in its presence.
Resistance to change
According to behavioral momentum theory, there are two separable aspects of the discriminated operant that independently govern the rate at which a response occurs and the persistence of that response in the face of operant disruption such as punishment, extinction, differential reinforcement of alternative behaviors, etc. (see Nevin & Grace, 2000, for a review). The positive reinforcement contingency between the response and a reinforcing consequence governs response rates (i.e., a response–reinforcer relation) by shaping a particular special pattern of responding, according to the relative law of non-absolute effect (i.e., the matching law; Herrnstein, 1970). Conversely, the Pavlovian relation established between the context (as a discriminative stimulus) and the rate or magnitude (but not both) of reinforcement obtained in the context (i.e., a stimulus–reinforcer relation) governs the resistance of the behavior class to behavioral operations such as implementing an extinction contingency. Resistance to change is assessed as responding during conditions of environmental disruption (e.g., satiation, extinction) relative to stable, pre-disruption behavior response rates.
Resistance to disruption has been considered a superior measure to stable response rates as an expression of the underlying strength of a response (Nevin, 1974). This is because drastic differences in response rates can occur by reinforcement contingency shaping particular patterns of behavior (e.g., differential-reinforcement-of-high- or low-response-rate schedules) while reinforcement rates are equal. It is unclear, therefore, whether these differences in response rates necessarily indicate differences in the underlying strength of a response (see Morse, 1966, for a discussion).
According to behavioral momentum theory, the relation between response rates and resistance to change is analogous to the velocity and mass of a moving object, according to Newton's second law of motion (Nevin, Mandell & Atak, 1983). Newton's second law states that the change in velocity of a moving object when an outside force is applied is directly related to that force and inversely related to the object's mass. Similarly, behavioral momentum theory states that the change in response rates under conditions of disruption (Bx) relative to baseline response rates (Bo) are directly related to the force or magnitude of disruption (f) and inversely related to the rate of reinforcement in a stimulus context (r):
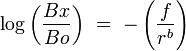 (1)
(1)
The free parameter b indicates the sensitivity of resistance to change to the rate of reinforcement in the stimulus context (i.e., the stimulus–reinforcer relation). Resistance to disruption typically is assessed when two distinctive discriminative stimulus contexts alternate and signal different schedules of reinforcement (i.e., a multiple schedule). Equation 1 can be rewritten to account for resistance to change across two stimulus contexts (Nevin, 1992; Nevin, Grace, & McLean, 2001) when a disrupter is uniformly applied across contexts (i.e., f1 = f2):
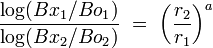 (2)
(2)
The subscripts indicate the different stimulus contexts. Thus, Equation 2 states that relative resistance to change is a power function of the relative rate of reinforcement across stimulus contexts, with the a parameter indicating sensitivity to relative reinforcement rate. Consistent with behavioral momentum theory, resistance to disruption often has been found to be greater in stimulus contexts presenting higher rates or magnitudes of reinforcement (see Nevin, 1992, for a review). Strong support for resistance to change being determined by stimulus–reinforcer relations and independent of response–reinforcer relations comes from studies that add response-independent (i.e., free) reinforcement to one stimulus context. For instance, Nevin, Tota, Torquato, and Shull (1990) had pigeons pecking lighted disks on separate variable-interval 60-s schedules of intermittent food reinforcement across two components of a multiple schedule. Additional free reinforcers were presented every 15 or 30 s on average when the disk was red, but not when the disk was green. Thus, the response–reinforcer relation was degraded when the disk was red because each reinforcer was not immediately preceded by a response. Consistent with the matching law, response rates were lower in the red context than in the green context. However, the stimulus–reinforcer relation was enhanced in the red context because the overall rate of food presentation was greater. Consistent with behavioral momentum theory, resistance to presession feeding (satiation) and discontinuing reinforcement in both contexts (extinction) was greater in the red context. Similar results have been found when reinforcers are added to a context by reinforcing an alternative response.
The findings of Nevin et al. (1990) have been extended across a number of procedures and species including goldfish (Igaki & Sakagami, 2004), rats (Harper, 1999a, 1999b; Shull, Gaynor & Grimes, 2001), pigeons (Podlesnik & Shahan, 2008), and humans (Ahearn, Clark, Gardenier, Chung & Dube, 2003; Cohen, 1996; Mace et al., 1990). The behavioral momentum framework also has been used to account for the partial-reinforcement extinction effect (Nevin & Grace, 1999), to assess the persistence of drug-maintained behavior (Jimenez-Gomez & Shahan, 2007; Shahan & Burke, 2004), to increase task compliance (e.g., Belfiore, Lee, Scheeler & Klein, 2002), and to understand the effects of social policies on global problems (Nevin, 2005).
Although behavioral momentum theory is a powerful framework for understanding how a context of reinforcement can affect the persistence of discriminated operant behavior, there are a number of findings that are inconsistent with the theory (see Nevin & Grace, 2000, and accompanying commentary). For instance, with equal reinforcement rates across stimulus contexts, resistance to change has been shown to be affected by manipulations to response–reinforcer relations, including schedules that produce different baseline response rates (e.g., Lattal, 1989; Nevin, Grace, Holland & McLean), delays to reinforcement (e.g., Bell, 1999; Grace, Schwendimann & Nevin, 1998; Podlesnik, Jimenez-Gomez, Ward & Shahan, 2006; Podlesnik & Shahan, 2008), and by providing brief stimuli that accompany reinforcement (Reed & Doughty, 2005). Also, it is unclear what factors affect relative resistance to change of responding maintained by conditioned reinforcement (Shahan & Podlesnik, 2005) or two concurrently available responses when different rates of reinforcement are arranged within the same context for those responses (e.g., Bell & Williams, 2002).
Preference and resistance to change
As resistance to disruption across stimulus contexts is analogous to the inertial mass of a moving object, behavioral momentum theory also suggests that preference in concurrent-chains procedures for one stimulus context over another is analogous to the gravitational attraction of two bodies (see Nevin & Grace, 2000). In concurrent-chains procedures, responding on the concurrently available initial links provides access to one of two mutually exclusive stimulus contexts called terminal links. As with multiple schedules, independent schedules of reinforcement can function in each terminal-link context. The relative allocation of responding across the two initial links indicates the extent to which an organism prefers one terminal-link context over the other. Moreover, behavioral momentum theory posits that preference provides a measure of the relative conditioned-reinforcing value of the two terminal-link contexts, as described by the contextual-choice model (Grace, 1994).
Grace and Nevin (1997) assessed both relative resistance to change in a multiple schedule and preference in a concurrent-chains procedure with pigeons pecking lighted disks for food reinforcement. When the relative rate of reinforcement was manipulated identically and simultaneously across stimulus contexts in the multiple schedule and concurrent-chains procedure, both relative resistance to change and preference was greater with richer contexts of reinforcement. When all the extant resistance to change and preference data were summarized by Grace, Bedell, and Nevin (2002), they found that those measures were related by a structural relation slope of 0.29. Therefore, relative resistance to change and preference both have been conceptualized as expressions of an underlying construct termed response strength, conditioned reinforcement value, or more generally, behavioral mass of discriminated operant behavior (see Nevin & Grace, 2000).
References
- Ahearn, W.H.; Clark, K.M.; Gardenier, N.C.; Chung, B.I. & Dube, W.V. (2003). Persistence of stereotyped behavior: Examining the effects of external reinforcers. Journal of Applied Behavior Analysis, 36, 439–448.
- Belfiore, P.J.; Lee, D.L.; Scheeler, C. & Klein, D. (2002). Implications of behavioral momentum and academic achievement for students with behavior disorders: Theory, application, and practice. Psychology in the Schools, 39, 171–179.
- Bell, M.C. (1999). Pavlovian contingencies and resistance to change in a multiple schedule. Journal of the Experimental Analysis of Behavior, 72, 81–96.
- Bell, M.C. & Williams, B.A. (2002). Preference and resistance to change in concurrent variable-interval schedules. Animal Learning & Behavior, 30, 34–42.
- Cohen, S.L. (1996). Behavioral momentum of typing behavior in college students. Journal of Behavior Analysis and Therapy, 1, 36–51.
- Dube, W.V.; Ahearn, W.H; Lionello-DeNolf, K. & McIlvane, W.J. (2009). Behavioral Momentum: Translational Research in Intellectual and Developmental Disabilities. The Behavior Analyst Today, 10(2), 238–253. BAO
- Grace, R.C. (1994). Independence of reinforcement delay and magnitude in concurrent chains. Journal of the Experimental Analysis of Behavior, 63, 255–276.
- Grace, R.C.; Bedell, M.A. & Nevin, J.A. (2002). Preference and resistance to change with constant- and variable-duration terminal links: Independence of reinforcement rate and magnitude. Journal of the Experimental Analysis of Behavior, 77, 233–255.
- Grace, R.C. & Nevin, J.A. (1997). On the relation between preference and resistance to change. Journal of the Experimental Analysis of Behavior, 67, 43–65.
- Grace, R.C.; Schwendiman, J.W. & Nevin, J.A. (1998). Effects of unsignaled delay of reinforcement on preference and resistance to change. Journal of the Experimental Analysis of Behavior, 69, 247–261.
- Harper, D.N. (1999a). Behavioral resistance to haloperidol and clozapine. Behavioral Processes, 46, 1–13.
- Harper, D.N. (1999b). Drug-induced changes in responding are dependent on baseline stimulus-reinforcer contingencies. Psychobiology, 27, 95–104.
- Herrnstein, R.J. (1970). On the law of effect. Journal of the Experimental Analysis of Behavior, 13, 243–266.
- Igaki, T. & Sakagami, T. (2004). Resistance to change in goldfish. Behavioral Processes, 66, 139–152.
- Jimenez-Gomez, C. & Shahan, T.A. (2007). Resistance to change of alcohol self-administration: Effects of alcohol-delivery rate on disruption by extinction and naltrexone. Behavioural Pharmacology, 18, 161–169.
- Lattal, K.A. (1989). Contingencies on response rate and resistance to change. Learning and Motivation, 20, 191–203.
- Mace, F.C.; Lalli, J.S.; Shea, M.C.; Lalli, E.P.; West, B.J.; Roberts, M. & Nevin, J.A. (1990). The momentum of human behavior in a natural setting. Journal of the Experimental Analysis of Behavior, 54, 163–172.
- Morse, W.H. (1966). Intermittent reinforcement. In W.K. Honig (Ed.), Operant behavior: Areas of research and application (pp. 52–108). New York: Appleton-Century Crofts.
- Nevin, J.A. (1974). Response strength in multiple schedules. Journal of the Experimental Analysis of Behavior, 21, 389–408.
- Nevin, J.A. (1992). An integrative model for the study of behavioral momentum. Journal of the Experimental Analysis of Behavior, 57, 301–316.
- Nevin, J.A. (2005). The inertia of affluence. Behavior and Social Issues, 14, 7-20.
- Nevin, J.A. & Grace, R.C. (1999). Does the context of reinforcement affect resistance to change? Journal of Experimental Psychology: Animal Behavior Processes, 25, 256–268.
- Nevin, J.A. & Grace, R.C. (2000a). Behavioral momentum and the Law of Effect. Behavioral and Brain Sciences, 23, 73–130.
- Nevin, J.A.; Grace, R.C.; Holland, S. & McLean, A.P. (2001). Variable-ratio versus variable-interval schedules: Response rate, resistance to change, and preference. Journal of the Experimental Analysis of Behavior, 76, 43–74.
- Nevin, J.A.; Grace, R.C. & McLean, A.P. (2001). Resistance to extinction: Contingency termination and generalization decrement. Journal of the Experimental Analysis of Behavior, 76, 43–74.
- Nevin, J.A.; Tota, M.E.; Torquato, R.D. & Shull, R.L. (1990). Alternative reinforcement increases resistance to change: Pavlovian or operant contingencies? Journal of the Experimental Analysis of Behavior, 53, 359–379.
- Podlesnik, C.A.; Jimenez-Gomez, C.; Ward, R.D. & Shahan, T.A. (2006). Resistance to change of responding maintained by unsignaled delays to reinforcement: A response-bout analysis. Journal of the Experimental Analysis of Behavior, 85, 329–347.
- Podlesnik, C.A. & Shahan, T.A. (2008). Response-reinforcer relations and resistance to change. Behavioural Processes, 77, 109–125.
- Reed, P. & Doughty, A.H. (2005). Within-subject testing of the signaled-reinforcement effect on operant responding as measured by response rate and resistance to change. Journal of the Experimental Analysis of Behavior, 83, 31–45.
- Shahan, T.A. & Burke, K.A. (2004). Ethanol-maintained responding of rats is more resistant to change in a context with added non-drug reinforcement. Behavioral Pharmacology, 15, 279–285.
- Shahan, T.A. & Podlesnik, C.A. (2005). Rate of conditioned reinforcement affects observing rate but not resistance to change. Journal of the Experimental Analysis of Behavior, 84, 1–17.
- Shull, R.L.; Gaynor, S.T. & Grimes, J.A. (2002). Response rate viewed as engagement bouts: Resistance to extinction. Journal of the Experimental Analysis of Behavior, 77, 211–231.
- Skinner, B.F. (1938). The behavior of organisms: An experimental analysis. Cambridge, MA: Appleton-Century-Crofts.
- Strand, P.S. (2001) Momentum, Matching, and Meaning: Toward a Fuller Exploitation of Operant Principles. The Behavior Analyst Today, 2(3), 170–175 BAO