Behavior of DEVS
Behaviors of a given DEVS model is a set of sequences of timed events including null events, called event segments which make the model move one state to another within a set of legal states. To define this way, the concept of a set of illegal state as well a set of legal states are needed to be introduced.
In addition, since the behaviors of a given DEVS model needs to define how the state transition change both when time is passed by and when an event occurs, it has been described by a much general formalism, called general system [ZPK00]. In this article, we use a sub-class of General System formalism, called timed event system instead.
Depending on how to define the total state and its external state transition function of DEVS, two ways to define the behavior of a DEVS model using Timed Event System. Since behavior of a coupled DEVS model is defined as an atomic DEVS model, behavior of coupled DEVS class is defined by timed event system.
View 1: total states = states * elapsed times
Suppose that a DEVS model,
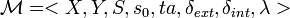 has
has
- the external state transition
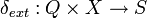 .
. - the total state set
![Q=\{(s,t_e)| s \in S, t_e \in (\mathbb{T} \cap [0, ta(s)])\}](../I/m/a7c7b1381d4bb7f8d8fc16a142d5e186.png) where
where 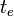 denotes elapsed time since last event and
denotes elapsed time since last event and 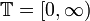 denotes the set of non-negative real numbers, and
denotes the set of non-negative real numbers, and
Then the DEVS model,
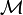 is a Timed Event System
is a Timed Event System 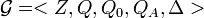 where
where
- The event set
.
- The state set
where
.
- The set of initial states
.
- The set of accepting states
- The set of state trajectories
is defined for two different cases:
and
. For an non-accepting state
, there is no change together with any even segment
so
For a total state
at time
and an event segment
as follows.
If unit event segment
is the null event segment, i.e.
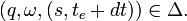
If unit event segment
is a timed event
where the event is an input event
,
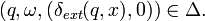
If unit event segment
is a timed event
where the event is an output event or the unobservable event
,
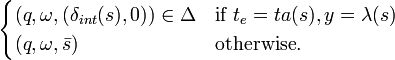
Computer algorithms to simulate this view of behavior are available at Simulation Algorithms for Atomic DEVS.
View 2: total states = states * lifespans * elapsed times
Suppose that a DEVS model,
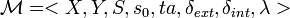 has
has
- the total state set
![Q=\{(s,t_s, t_e)| s \in S, t_s\in \mathbb{T}^\infty, t_e \in (\mathbb{T} \cap [0, t_s])\}](../I/m/e62e696d5aabb7d72ddbe5d787c4332c.png) where
where 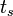 denotes lifespan of state
denotes lifespan of state  ,
, 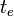 denotes elapsed time since last
denotes elapsed time since last 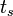 update, and
update, and 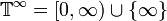 denotes the set of non-negative real numbers plus infinity,
denotes the set of non-negative real numbers plus infinity, - the external state transition is
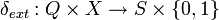 .
.
Then the DEVS 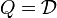 is a timed event system
is a timed event system 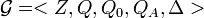 where
where
- The event set
.
- The state set
where
.
- The set of initial states
.
- The set of acceptance states
.
- The set of state trajectories
is depending on two cases:
and
. For a non-accepting state
, there is no changes together with any segment
so
For a total state
at time
and an event segment
as follows.
If unit event segment
is the null event segment, i.e.
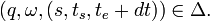
If unit event segment
is a timed event
where the event is an input event
,
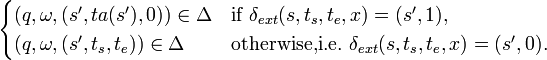
If unit event segment
is a timed event
where the event is an output event or the unobservable event
,
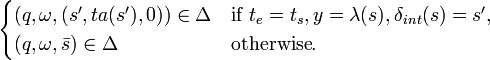
Computer algorithms to simulate this view of behavior are available at Simulation Algorithms for Atomic DEVS.
Comparison of View1 and View2
Features of View1
View1 has been introduced by Zeigler [Zeigler84] in which given a total state 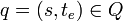 and
and
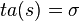
where  is the remaining time [Zeigler84] [ZPK00]. In other words, the set of partial states is indeed
is the remaining time [Zeigler84] [ZPK00]. In other words, the set of partial states is indeed 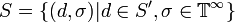 where
where 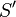 is a state set.
is a state set.
When a DEVS model receives an input event 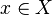 , View1 resets the elapsed time
, View1 resets the elapsed time 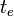 by zero, if the DEVS model needs to ignore
by zero, if the DEVS model needs to ignore  in terms of the lifespan control, modellers have to update the remaining time
in terms of the lifespan control, modellers have to update the remaining time
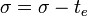
in the external state transition function 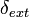 that is the responsibility of the modellers.
that is the responsibility of the modellers.
Since the number of possible values of  is the same as the number of possible input events coming to the DEVS model, that is unlimited. As a result, the number of states
is the same as the number of possible input events coming to the DEVS model, that is unlimited. As a result, the number of states 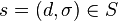 is also unlimited that is the reason why View2 has been proposed.
is also unlimited that is the reason why View2 has been proposed.
If we don't care the finite-vertex reachability graph of a DEVS model, View1 has an advantage of simplicity for treating the elapsed time 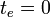 every time any input event arrives into the DEVS model. But disadvantage might be modelers of DEVS should know how to manage
every time any input event arrives into the DEVS model. But disadvantage might be modelers of DEVS should know how to manage  as above, which is not explicitly explained in
as above, which is not explicitly explained in  itself but in
itself but in  .
.
Features of View2
View2 has been introduced by Hwang and Zeigler[HZ06][HZ07] in which given a total state 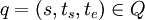 , the remaining time,
, the remaining time,  is computed as
is computed as
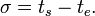
When a DEVS model receives an input event 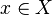 , View2 resets the elapsed time
, View2 resets the elapsed time 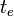 by zero only if
by zero only if 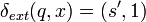 . If the DEVS model needs to ignore
. If the DEVS model needs to ignore  in terms of the lifespan control, modellers can use
in terms of the lifespan control, modellers can use 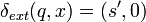 .
.
Unlike View1, since the remaining time  is not component of
is not component of  in nature, if the number of states, i.e.
in nature, if the number of states, i.e. 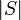 is finite, we can draw a finite-vertex (as well as edge) state-transition diagram [HZ06][HZ07]. As a result, we can abstract behavior of such a DEVS-class network, for example SP-DEVS and FD-DEVS, as a finite-vertex graph, called reachability graph [HZ06][HZ07].
is finite, we can draw a finite-vertex (as well as edge) state-transition diagram [HZ06][HZ07]. As a result, we can abstract behavior of such a DEVS-class network, for example SP-DEVS and FD-DEVS, as a finite-vertex graph, called reachability graph [HZ06][HZ07].
See also
- Behavior of Coupled DEVS
- Simulation Algorithms for Atomic DEVS
- Simulation Algorithms for Coupled DEVS
References
- [Zeigler76] Bernard Zeigler (1976). Theory of Modeling and Simulation (first ed.). Wiley Interscience, New York.
- [Zeigler84] Bernard Zeigler (1984). Multifacetted Modeling and Discrete Event Simulation. Academic Press, London; Orlando. ISBN 978-0-12-778450-2.
- [ZKP00] Bernard Zeigler, Tag Gon Kim, Herbert Praehofer (2000). Theory of Modeling and Simulation (second ed.). Academic Press, New York. ISBN 978-0-12-778455-7.
- [HZ06] M. H. Hwang and Bernard Zeigler, ``A Reachable Graph of Finite and Deterministic DEVS Networks``, Proceedings of 2006 DEVS Symposium, pp48-56, Huntsville, Alabama, USA, (Available at http://www.acims.arizona.edu and http://moonho.hwang.googlepages.com/publications)
- [HZ07] M.H. Hwang and Bernard Zeigler, ``Reachability Graph of Finite & Deterministic DEVS``, IEEE Transactions on Automation Science and Engineering, Volume 6, Issue 3, 2009, pp.454–467, http://ieeexplore.ieee.org/xpl/freeabs_all.jsp?isnumber=5153598&arnumber=5071137&count=19&index=7
![\omega=\epsilon_{[t, t+dt]}](../I/m/021f89f2c31c7ba635873d2725564100.png)