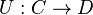Beck's monadicity theorem

In category theory, a branch of mathematics, Beck's monadicity theorem gives a criterion that characterises monadic functors. It asserts that a functor

U: C \to D

is monadic if and only if[1]

  1. U has a left adjoint;
  2. U reflects isomorphisms; and
  3. C has coequalizers of U-split parallel pairs (those parallel pairs of morphisms in C, which U sends to pairs having a split coequalizer in D), and U preserves those coequalizers.

The second and third condition together can be replaced by a modified condition: every fork in C which is by U sent to a split coequalizer sequence in D is itself a coequalizer sequence in C. In different words, U creates (preserves and reflects) U-split coequalizer sequences.

This is a basic result of Jonathan Mock Beck from around 1967, often stated in dual form for comonads. It is also sometimes called the Beck tripleability theorem because of the older term triple for a monad.

This theorem is particularly important in its relation with the descent theory, which plays role in sheaf and stack theory, as well as in the Grothendieck's approach to algebraic geometry. Most cases of faithfully flat descent of algebraic structures (e.g. those in FGA and in SGA1) are special cases of Beck's theorem. The theorem gives an exact categorical description of the process of 'descent', at this level. In 1970 the Grothendieck approach via fibered categories and descent data was shown (by Bénabou and Roubaud) to be equivalent (under some conditions) to the comonad approach. In a later work, Pierre Deligne applied Beck's theorem to Tannakian category theory, greatly simplifying the basic developments.

References

  1. ↑ Pedicchio & Tholen (2004) p.228

External links