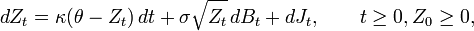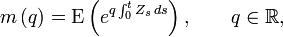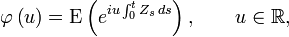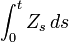Basic affine jump diffusion

In probability theory, a basic affine jump diffusion (basic AJD) is a stochastic process Z of the form

dZ_t=\kappa (\theta -Z_t)\,dt+\sigma \sqrt{Z_t}\,dB_t+dJ_t,\qquad t\geq 0, Z_{0}\geq 0,

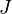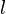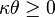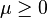where $B$ is a standard Brownian motion, and $J$ is an independent compound Poisson process with constant jump intensity $l$ and independent exponentially distributed jumps with mean $\mu$ . For the process to be well defined, it is necessary that $\kappa \theta \geq 0$ and $\mu \geq 0$ . A basic AJD is a special case of an affine process and of a jump diffusion. On the other hand, the Cox–Ingersoll–Ross (CIR) process is a special case of a basic AJD.

Basic AJDs are attractive for modeling default times in credit risk applications,^[1]^[2]^[3]^[4] since both the moment generating function

m\left( q\right) =\operatorname{E} \left( e^{q\int_0^t Z_s \, ds}\right) ,\qquad q\in \mathbb{R},

and the characteristic function

\varphi \left( u\right) =\operatorname{E} \left( e^{iu\int_0^t Z_s \, ds}\right) ,\qquad u\in \mathbb{R},

are known in closed form.^[3]

The characteristic function allows one to calculate the density of an integrated basic AJD

\int_0^t Z_s \, ds

by Fourier inversion, which can be done efficiently using the FFT.

References

↑ Darrell Duffie, Nicolae Gârleanu (2001). "Risk and Valuation of Collateralized Debt Obligations". Financial Analysts Journal 57: 41–59. doi:10.2469/faj.v57.n1.2418. Preprint
↑ Allan Mortensen (2006). "Semi-Analytical Valuation of Basket Credit Derivatives in Intensity-Based Models". Journal of Derivatives 13: 8–26. doi:10.3905/jod.2006.635417. Preprint
↑ 3.0 3.1 Andreas Ecker (2009). "Computational Techniques for basic Affine Models of Portfolio Credit Risk". Journal of Computational Finance 13: 63–97.
↑ Peter Feldhütter, Mads Stenbo Nielsen (2010). "Systematic and idiosyncratic default risk in synthetic credit markets". Preprint