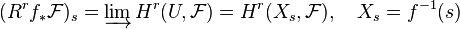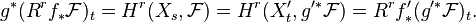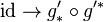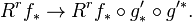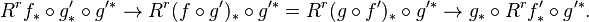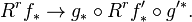Base change map

In mathematics, the base change map relates the direct image and the pull-back of sheaves. More precisely, it is the following natural transformation of sheaves:

g^*(R^r f_* \mathcal{F}) \to R^r f'_*(g'^*\mathcal{F})

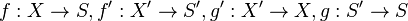where f: X \to S, f':X' \to S', g':X' \to X, g:S' \to S are continuous maps between topological spaces that form a Cartesian square and \mathcal{F} is a sheaf on X.

In general topology, the map is an isomorphism under some mild technical conditions. An analogous result holds for étale cohomologies (with topological spaces replaced by sites), though more difficult. See proper base change theorem.

General topology

If X is a Hausdorff topological space, S is a locally compact Hausdorff space and f is universally closed (i.e., 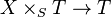X \times_S T \to T is closed for any continuous map 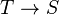T \to S), then the base change map is an isomorphism.[1] Indeed, we have: for 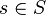s \in S,

(R^r f_* \mathcal{F})_s = \varinjlim H^r(U, \mathcal{F}) = H^r(X_s, \mathcal{F}), \quad X_s = f^{-1}(s)

and so for 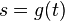s = g(t)

g^* (R^r f_* \mathcal{F})_t = H^r(X_s, \mathcal{F}) = H^r(X'_t, g'^* \mathcal{F}) = R^r f'_* (g'^* \mathcal{F})_t.

Derivation

Since 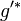g'^* is left adjoint to 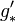g'_*, we have:

\operatorname{id} \to g'_* \circ g'^*

and so

R^r f_* \to R^r f_* \circ g'_* \circ g'^*.

The Grothendieck spectral sequence then gives the first map and the last map (they are edge maps) in:

R^r f_* \circ g'_* \circ g'^* \to R^r(f \circ g')_* \circ g'^* = R^r(g \circ f')_* \circ g'^* \to g_* \circ R^r f'_* \circ g'^*.

Combining this with the above we get

R^r f_* \to g_* \circ R^r f'_* \circ g'^*.

Again using the adjoint relation we get the desired map.

See also

References

  1. ↑ Milne, Theorem 17.3