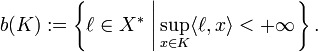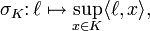Barrier cone

In mathematics, specifically functional analysis, the barrier cone is a cone associated to any non-empty subset of a Banach space. It is closely related to the notions of support functions and polar sets.

Definition

Let X be a Banach space and let K be a non-empty subset of X. The barrier cone of K is the subset b(K) of X^∗, the continuous dual space of X, defined by

b(K) := \left\{ \ell \in X^{\ast} \,\left|\, \sup_{x \in K} \langle \ell, x \rangle < + \infty \right. \right\}.

Related notions

The function

\sigma_{K} \colon \ell \mapsto \sup_{x \in K} \langle \ell, x \rangle,

defined for each continuous linear functional ℓ on X, is known as the support function of the set K; thus, the barrier cone of K is precisely the set of continuous linear functionals ℓ for which σ_K(ℓ) is finite.

The set of continuous linear functionals ℓ for which σ_K(ℓ) ≤ 1 is known as the polar set of K. The set of continuous linear functionals ℓ for which σ_K(ℓ) ≤ 0 is known as the (negative) polar cone of K. Clearly, both the polar set and the negative polar cone are subsets of the barrier cone.

References

Aubin, Jean-Pierre; Frankowska, Hélène (2009). Set-Valued Analysis (Reprint of the 1990 ed.). Boston, MA: Birkhäuser Boston Inc. pp. xx+461. ISBN 978-0-8176-4847-3. MR 2458436.