Barrelled space

In functional analysis and related areas of mathematics, barrelled spaces are Hausdorff topological vector spaces for which every barrelled set in the space is a neighbourhood for the zero vector. A barrelled set or a barrel in a topological vector space is a set which is convex, balanced, absorbing and closed. Barrelled spaces are studied because a form of the Banach–Steinhaus theorem still holds for them.

History

Barrelled spaces were introduced by Bourbaki (1950).

Examples

• In a semi normed vector space the closed unit ball is a barrel.
• Every locally convex topological vector space has a neighbourhood basis consisting of barrelled sets, although the space itself need not be a barreled space.
• Fréchet spaces, and in particular Banach spaces, are barrelled, but generally a normed vector space is not barrelled.
• Montel spaces are barrelled. Consequently, strong duals of Montel spaces are barrelled (since they are Montel spaces).
• locally convex spaces which are Baire spaces are barrelled.

Properties

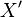For a Hausdorff locally convex space with continuous dual the following are equivalent:

• X is barrelled,
• every -bounded subset of the continuous dual space X' is equicontinuous (this provides a partial converse to the Banach-Steinhaus theorem),^[1]
• for all subsets A of the continuous dual space X', the following properties are equivalent: A is ^[1]
  • equicontinuous,
  • relatively weakly compact,
  • strongly bounded,
  • weakly bounded,
• X carries the strong topology ,
• every lower semi-continuous semi-norm on is continuous,
• the 0-neighborhood bases in X and the fundamental families of bounded sets in 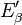correspond to each other by polarity.^[1]

In addition,

• Every sequentially complete quasibarrelled space is barrelled.
• A barrelled space need not be Montel, complete, metrizable, unordered Baire-like, nor the inductive limit of Banach spaces.

Quasi-barrelled spaces

A topological vector space for which every barrelled bornivorous set in the space is a neighbourhood of is called a quasi-barrelled space, where a set is bornivorous if it absorbs all bounded subsets of . Every barrelled space is quasi-barrelled.

For a locally convex space with continuous dual 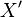the following are equivalent:

• is quasi-barrelled,
• every bounded lower semi-continuous semi-norm on is continuous,
• every 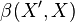-bounded subset of the continuous dual space 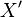is equicontinuous.

References

1. ↑ 1.0 1.1 1.2 Schaefer (1999) p. 127, 141, Treves (1995) p. 350

• Bourbaki, Nicolas (1950). "Sur certains espaces vectoriels topologiques". Annales de l'Institut Fourier (in French) 2: 5–16 (1951). MR 0042609. 
• Robertson, Alex P.; Robertson, Wendy J. (1964). Topological vector spaces. Cambridge Tracts in Mathematics 53. Cambridge University Press. pp. 65–75. 
• Schaefer, Helmut H. (1971). Topological vector spaces. GTM 3. New York: Springer-Verlag. p. 60. ISBN 0-387-98726-6. 
• S.M. Khaleelulla (1982). Counterexamples in Topological Vector Spaces. GTM 936. Springer-Verlag. pp. 28–46. ISBN 978-3-540-11565-6.