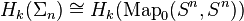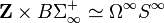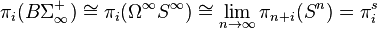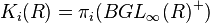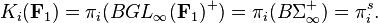Barratt–Priddy theorem

In homotopy theory, a branch of mathematics, the Barratt–Priddy theorem (also referred to as Barratt–Priddy–Quillen theorem) expresses a connection between the homology of the symmetric groups and mapping spaces of spheres. It is also often stated as a relation between the sphere spectrum and the classifying spaces of the symmetric groups via Quillen's plus construction.

Statement of the theorem

The mapping space $Map 0 (S n, S n)$ is the topological space of all continuous maps $f : S n \to S n$ from the $n$ -dimensional sphere $S n$ to itself, under the topology of uniform convergence (a special case of the compact-open topology). These maps are required to fix a basepoint $x \in S n$ , satisfying $f (x)= x$ , and to have degree 0; this guarantees that the mapping space is connected. The Barratt–Priddy theorem expresses a relation between the homology of these mapping spaces and the homology of the symmetric groups $Σ n$ .

It follows from the Freudenthal suspension theorem and the Hurewicz theorem that the $k$ th homology $H k (Map 0 (S n, S n))$ of this mapping space is independent of the dimension $n$ , as long as $n > k$ . Similarly, Nakaoka (1960) proved that the $k$ th group homology $H k (Σ n)$ of the symmetric group $Σ n$ on $n$ elements is independent of $n$ , as long as $n \geq2 k$ .

The Barratt–Priddy theorem states that these "stable homology groups" are the same: for $n \geq2 k$ there is a natural isomorphism

H_k(\Sigma_n)\cong H_k(\text{Map}_0(S^n,S^n))

This isomorphism holds with integral coefficients (in fact with any coefficients, as is made clear in the reformulation below).

Example: first homology

This isomorphism can be seen explicitly for the first homology $H 1$ . The first homology of a group is the largest commutative quotient of that group. For the permutation groups $Σ n$ , the only commutative quotient is given by the sign of a permutation, taking values in ${-1, 1$ }. This shows that $H 1 (Σ n)≅ Z /2 Z$ , the cyclic group of order 2, for all $n \geq2$ . (For $n =1$ , $Σ 1$ is the trivial group, so $H 1 (Σ n)=0$ .)

It follows from the theory of covering spaces that the mapping space $Map 0 (S 1, S 1)$ of the circle $S 1$ is contractible, so $H 1 (Map 0 (S 1, S 1))=0$ . For the 2-sphere $S 2$ , the first homotopy group and first homology group of the mapping space are both infinite cyclic: $π 1 (Map 0 (S 2, S 2))≅ H 1 (Map 0 (S 2, S 2))≅ Z$ . A generator for this group can be built from the Hopf fibration $S 3 \to S 2$ . Finally, once $n \geq3$ , both are cyclic of order 2: $π 1 (Map 0 (S n, S n))≅ H 1 (Map 0 (S n, S n))$ ≅Z/2Z.

Reformulation of the theorem

The infinite symmetric group $Σ \infty$ is the union of the finite symmetric groups $Σ n$ , and Nakaoka's theorem implies that the group homology of $Σ \infty$ is the stable homology of $Σ n$ : for $n \geq2 k$ , $H k (Σ \infty)≅ H k (Σ n)$ . The classifying space of this group is denoted $BΣ \infty$ , and its homology of this space is the group homology of $Σ \infty$ : $H k (BΣ \infty)≅ H k (Σ \infty)$ .

We similarly denote by $Map 0 (S \infty, S \infty)$ the union of the mapping spaces $Map 0 (S n, S n)$ (under the inclusions induced by suspension). The homology of $Map 0 (S \infty, S \infty)$ is the stable homology of the previous mapping spaces: for $n > k$ , $H k (Map 0 (S \infty, S \infty))≅ H k (Map 0 (S n, S n))$ .

There is a natural map $φ : BΣ \infty \toMap 0 (S \infty, S \infty)$ (one way to construct $φ$ is via the model of $BΣ \infty$ as the space of finite subsets of $R \infty$ endowed with a certain topology). An equivalent formulation of the Barratt–Priddy theorem is that $φ$ is a homology equivalence (or acyclic map), meaning that $φ$ induces an isomorphism on all homology groups with any local coefficient system.

Relation with Quillen's plus construction

The Barratt–Priddy theorem implies that the space $BΣ \infty +$ resulting from applying Quillen's plus construction to $BΣ \infty$ can be identified with $Map 0 (S \infty, S \infty)$ . (Since $π 1 (Map 0 (S \infty, S \infty))≅ H 1 (Σ \infty)≅ Z /2 Z$ , the map $φ : BΣ \infty \toMap 0 (S \infty, S \infty)$ satisfies the universal property of the plus construction once it is known that $φ$ is a homology equivalence.)

The mapping spaces $Map 0 (S n, S n)$ are more commonly denoted by $Ω n 0 S n$ , where $Ω n S n$ is the $n$ -fold loop space of the $n$ -sphere $S n$ , and similarly $Map 0 (S \infty, S \infty)$ is denoted by $Ω \infty 0 S \infty$ . Therefore the Barratt–Priddy theorem can also be stated as

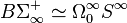B\Sigma_\infty^+\simeq \Omega_0^\infty S^\infty

\textbf{Z}\times B\Sigma_\infty^+\simeq \Omega^\infty S^\infty

In particular, the homotopy groups of $BΣ \infty +$ are the stable homotopy groups of spheres:

\pi_i(B\Sigma_\infty^+)\cong \pi_i(\Omega^\infty S^\infty)\cong \lim_{n\rightarrow \infty} \pi_{n+i}(S^n)=\pi_i^s

"K-theory of F₁"

The Barratt–Priddy theorem is sometimes colloquially rephrased as saying that "the K-groups of F₁ are the stable homotopy groups of spheres". This is not a meaningful mathematical statement, but a metaphor expressing an analogy with algebraic K-theory.

The "field with one element" F₁ is not a mathematical object; it refers to a collection of analogies between algebra and combinatorics. One central analogy is the idea that $GL n (F 1)$ should be the symmetric group $Σ n$ . The higher K-groups $K i (R)$ of a ring R can be defined as

K_i(R)=\pi_i(BGL_\infty(R)^+)

According to this analogy, the K-groups $K i (F 1)$ of $F 1$ should be defined as $π i (BGL \infty (F 1) +)= π i (BΣ \infty +)$ , which by the Barratt–Priddy theorem is:

K_i(\mathbf{F}_1)=\pi_i(BGL_\infty(\mathbf{F}_1)^+)=\pi_i(B\Sigma_\infty^+)=\pi_i^s.

References

Barratt, Michael; Priddy, Stewart (1972), "On the homology of non-connected monoids and their associated groups", Commentarii Mathematici Helvetici 47: 1–14, doi:10.1007/bf02566785, ISSN 0010-2571

Nakaoka, Minoru (1960), "Decomposition theorem for homology groups of symmetric groups", Annals of Mathematics 71: 16–42, doi:10.2307/1969878, MR 112134