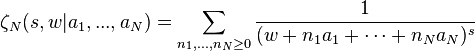Barnes zeta function
In mathematics, a Barnes zeta function is a generalization of the Riemann zeta function introduced by E. W. Barnes (1901). It is further generalized by the Shintani zeta function.
Definition
The Barnes zeta function is defined by
where w and aj have positive real part and s has real part greater than N.
It has a meromorphic continuation to all complex s, whose only singularities are simple poles at s = 1, 2, ..., N. For N = w = a1 = 1 it is the Riemann zeta function.
References
- Barnes, E. W. (1899), "The Theory of the Double Gamma Function. [Abstract]", Proceedings of the Royal Society of London (The Royal Society) 66: 265–268, doi:10.1098/rspl.1899.0101, ISSN 0370-1662, JSTOR 116064
- Barnes, E. W. (1901), "The Theory of the Double Gamma Function", Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character (The Royal Society) 196: 265–387, doi:10.1098/rsta.1901.0006, ISSN 0264-3952, JSTOR 90809
- Barnes, E. W. (1904), "On the theory of the multiple gamma function", Trans. Cambridge Philos. Soc. 19: 374–425
- Friedman, Eduardo; Ruijsenaars, Simon (2004), "Shintani–Barnes zeta and gamma functions", Advances in Mathematics 187 (2): 362–395, doi:10.1016/j.aim.2003.07.020, ISSN 0001-8708, MR 2078341
- Ruijsenaars, S. N. M. (2000), "On Barnes' multiple zeta and gamma functions", Advances in Mathematics 156 (1): 107–132, doi:10.1006/aima.2000.1946, ISSN 0001-8708, MR 1800255