Baire function
In mathematics, Baire functions are functions obtained from continuous functions by transfinite iteration of the operation of forming pointwise limits of sequences of functions. They were introduced by René-Louis Baire (1905). A Baire set is a set whose characteristic function is a Baire function (not necessarily of any particular class, as defined below).
Classification of Baire functions
Baire functions of class n, for any countable ordinal number n, form a vector space of real-valued functions defined on a topological space, as follows.
- The Baire class 0 functions are the continuous functions.
- The Baire class 1 functions are those functions which are the pointwise limit of a sequence of Baire class 0 functions.
- In general, the Baire class n functions are all functions which are the pointwise limit of a sequence of functions of Baire class less than n.
Some authors define the classes slightly differently, by removing all functions of class less than n from the functions of class n. This means that each Baire function has a well defined class, but the functions of given class no longer form a vector space.
Henri Lebesgue proved that (for functions on the unit interval) each Baire class of a countable ordinal number contains functions not in any smaller class, and that there exist functions which are not in any Baire class.
Baire class 1
Examples:
- The derivative of any differentiable function is of class 1. An example of a differentiable function whose derivative is not continuous (at x=0) is the function equal to
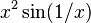when x≠0, and 0 when x=0. An infinite sum of similar functions (scaled and displaced by rational numbers) can even give a differentiable function whose derivative is discontinuous on a dense set. However, it necessarily has points of continuity, which follows easily from The Baire Characterisation Theorem (below; take K=X=R). - The function equal to 1 if x is an integer and 0 otherwise. (An infinite number of large discontinuities.)
- The function that is 0 for irrational x and 1/q for a rational number p/q (in reduced form). (A dense set of discontinuities, namely the set of rational numbers.)
- The characteristic function of the Cantor set, which gives 1 if x is in the Cantor set and 0 otherwise. This function is 0 for an uncountable set of x values, and 1 for an uncountable set. It is discontinuous wherever it equals 1 and continuous wherever it equals 0. It is approximated by the continuous functions
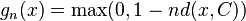, where 
is the distance of x from the nearest point in the Cantor set.
The Baire Characterisation Theorem states that a real valued function f defined on a Banach space X is a Baire-1 function if and only if for every non-empty closed subset K of X, the restriction of f to K has a point of continuity relative to the topology of K.
By another theorem of Baire, for every Baire-1 function the points of continuity are a comeager Gδset (Kechris 1995, Theorem (24.14)).
Baire class 2
Examples:
- An example of a Baire class two function on the interval [0,1] that is not of class 1 is the characteristic function of the rational numbers,
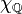, also known as the Dirichlet function. It is discontinuous everywhere.
Baire class 3
Examples:
See also
References
- Baire, R. (1905), Leçons sur les fonctions discontinues, professées au collège de France, Gauthier-Villars
- Kechris, Alexander S. (1995), Classical Descriptive Set Theory, Springer-Verlag