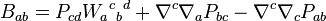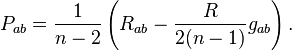Bach tensor
In differential geometry and general relativity, the Bach tensor is a trace-free tensor of rank 2 which is conformally invariant in dimension n = 4.[1] Before 1968, it was the only known conformally invariant tensor that is algebraically independent of the Weyl tensor.[2] In abstract indices the Bach tensor is given by
where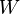 
is the Weyl tensor, and 
the Schouten tensor given in terms of the Ricci tensor 
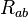and scalar curvature 
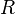by
See also
- Cotton tensor
- Obstruction tensor
References
- ↑ Rudolf Bach, "Zur Weylschen Relativitätstheorie und der Weylschen Erweiterung des Krümmungstensorbegriffs", Mathematische Zeitschrift, 9 (1921) pp. 110.
- ↑ P. Szekeres, Conformal Tensors. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences Vol. 304, No. 1476 (Apr. 2, 1968), pp. 113–122
Further reading
- Arthur L. Besse, Einstein Manifolds. Springer-Verlag, 2007. See Ch.4, §H "Quadratic Functionals".
- Demetrios Christodoulou, Mathematical Problems of General Relativity I. European Mathematical Society, 2008. Ch.4 §2 "Sketch of the proof of the global stability of Minkowski spacetime".
- Yvonne Choquet-Bruhat, General Relativity and the Einstein Equations. Oxford University Press, 2011. See Ch.XV §5 "Christodoulou-Klainerman theorem" which notes the Bach tensor is the "dual of the Coton tensor which vanishes for conformally flat metrics".
- Thomas W. Baumgarte, Stuart L. Shapiro, Numerical Relativity: Solving Einstein's Equations on the Computer. Cambridge University Press, 2010. See Ch.3.