Büchi arithmetic
Büchi arithmetic of base k is the first-order theory of the natural numbers with addition and the function 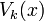 which is defined as the largest power of k dividing x, named in honor of the Swiss mathematician Julius Richard Büchi. The signature of Presburger arithmetic contains only the addition operation,
which is defined as the largest power of k dividing x, named in honor of the Swiss mathematician Julius Richard Büchi. The signature of Presburger arithmetic contains only the addition operation, 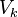 and equality, omitting the multiplication operation entirely.
and equality, omitting the multiplication operation entirely.
Unlike Peano arithmetic, Büchi arithmetic is a decidable theory. This means it is possible to effectively determine, for any sentence in the language of Büchi arithmetic, whether that sentence is provable from the axioms of Presburger arithmetic.
Büchi arithmetic and automaton
A subset 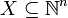 is definable in Bûchi arithmetic of base k if and only if it is k-recognisable.
is definable in Bûchi arithmetic of base k if and only if it is k-recognisable.
If 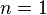 this means that the set of integers of X in base k is accepted by an automaton. Similarly if
this means that the set of integers of X in base k is accepted by an automaton. Similarly if 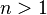 there exists an automata that read firsts digit, then second digits, and so on, of n integers in base k, and accept the words if the n integers are in the relation X.
there exists an automata that read firsts digit, then second digits, and so on, of n integers in base k, and accept the words if the n integers are in the relation X.
Properties of Büchi arithmetic
Two numbers k and l are multiplicatively dependent if there exists integers n and m such that 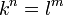 .
.
If k and l are multiplicatively dependent then Büchi arithmetic of base k and l have the same expressivity. Indeed 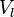 can be defined in
can be defined in 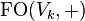 .
.
Else the theory with both 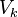 and
and 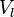 function is equivalent to Peano arithmetic the logic with addition and multiplication since multiplication is definable in
function is equivalent to Peano arithmetic the logic with addition and multiplication since multiplication is definable in 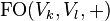 .
.
On the other hand by the Cobham–Semenov theorem, if a relation is definable in both k and l Büchi arithmetics it is definable in Presburger arithmetic.[1][2]
References
- ↑ Cobham, Alan (1969). "On the base-dependence of sets of numbers recognizable by finite automata". Math. Systems Theory 3: 186–192. doi:10.1007/BF01746527.
- ↑ Semenov, A. L. (1977). "Presburgerness of predicates regular in two number systems". Sibirsk. Mat. Zh. (in Russian) 18: 403–418.
- Bès, Alexis. "A survey of Arithmetical Definability". Retrieved 27 June 2012.
Further reading
- Bès, Alexis (1997). "Undecidable extensions of Büchi arithmetic and Cobham-Semënov theorem". J. Symb. Log. 62 (4): 1280–1296. doi:10.2307/2275643. Zbl 0896.03011.