Auxiliary field

In physics, and especially quantum field theory, an auxiliary field is one whose equations of motion admit a single solution. Therefore, the Lagrangian describing such a field $A$ contains an algebraic quadratic term and an arbitrary linear term, while it contains no kinetic terms (derivatives of the field):
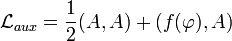$\mathcal{L}_{aux}=\frac{1}{2}(A,A)+(f(\varphi),A)$ .
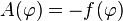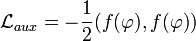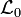The equation of motion for $A$ is: $A(\varphi)=-f(\varphi)$ and the Lagrangian becomes: $\mathcal{L}_{aux}=-\frac{1}{2}(f(\varphi),f(\varphi))$ . Auxiliary fields do not propagate and hence the content of any theory remains unchanged by adding such fields by hand. If we have an initial Lagrangian $\mathcal{L}_{0}$ describing a field 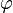$\varphi$ then the Lagrangian describing both fields is:
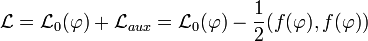$\mathcal{L}=\mathcal{L}_{0}(\varphi)+\mathcal{L}_{aux}=\mathcal{L}_{0}(\varphi)-\frac{1}{2}(f(\varphi),f(\varphi))$ .
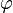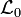Therefore, auxiliary fields can be employed to cancel quadratic terms in $\varphi$ in $\mathcal{L}_{0}$ and linearize the action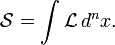 $\mathcal{S} = \int{\mathcal{L}\,d^nx}.$

Examples of auxiliary fields are the complex scalar field F in a chiral superfield, the real scalar field D in a vector superfield, the scalar field B in BRST and the field in the Hubbard-Stratonovich transformation.

The quantum mechanical effect of adding an auxiliary field is the same as the classical, since the path integral over such a field is Gaussian. To wit:

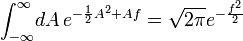\int_{-\infty}^\infty\!dA\, e^{-\frac{1}{2} A^2 + A f} = \sqrt{2\pi}e^{-\frac{f^2}{2}}

References

Superspace, or One thousand and one lessons in supersymmetry arXiv:hep-th/0108200