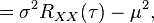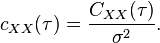Autocovariance
In probability and statistics, given a stochastic process 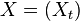 , the autocovariance is a function that gives the covariance of the process with itself at pairs of time points. With the usual notation E for the expectation operator, if the process has the mean function
, the autocovariance is a function that gives the covariance of the process with itself at pairs of time points. With the usual notation E for the expectation operator, if the process has the mean function ![\mu_t = E[X_t]](../I/m/457de2f54dd1239d3e9aa8d71d9ad946.png) , then the autocovariance is given by
, then the autocovariance is given by
Autocovariance is related to the more commonly used autocorrelation of the process in question.
In the case of a random vector 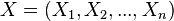 , the autocovariance would be a square n by n matrix
, the autocovariance would be a square n by n matrix 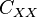 with entries
with entries 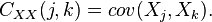 This is commonly known as the covariance matrix or matrix of covariances of the given random vector.
This is commonly known as the covariance matrix or matrix of covariances of the given random vector.
Stationarity
If X(t) is stationary process, then the following are true:
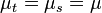 for all t, s
for all t, s
and
where
is the lag time, or the amount of time by which the signal has been shifted.
As a result, the autocovariance becomes
where 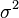 is the variance and
is the variance and 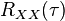 is the autocorrelation of the signal.
is the autocorrelation of the signal.
Normalization
When normalized by dividing by the variance σ2, the autocovariance C becomes the autocorrelation coefficient function c,[1]
However, often the autocovariance is called autocorrelation even if this normalization has not been performed.
The autocovariance can be thought of as a measure of how similar a signal is to a time-shifted version of itself with an autocovariance of σ2 indicating perfect correlation at that lag. The normalization with the variance will put this into the range [−1, 1].
Properties
The autocovariance of a linearly filtered process 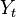
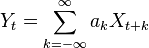
- is
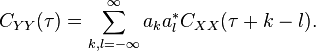
See also
- Autocorrelation
- Covariance and Correlation
- Covariance mapping
- Cross-covariance
- Cross-correlation
- Noise covariance estimation (as an application example)
References
- Hoel, P. G. (1984). Mathematical Statistics (Fifth ed.). New York: Wiley. ISBN 0-471-89045-6.
- Lecture notes on autocovariance from WHOI
![C_{XX}(t,s) = cov(X_t, X_s) = E[(X_t - \mu_t)(X_s - \mu_s)] = E[X_t X_s] - \mu_t \mu_s.\,](../I/m/eb7eea6bb5cf464ab581a258c0dba1a8.png)
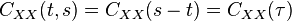
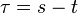
![C_{XX}(\tau) = E[(X(t) - \mu)(X(t+\tau) - \mu)]\,](../I/m/0a0f0b0322067c9d8ae3f934a2cf0dcb.png)
![= E[X(t) X(t+\tau)] - \mu^2\,](../I/m/cb52602daac4d4c667f5e678b70076d1.png)