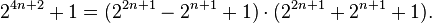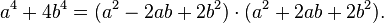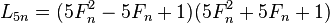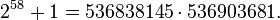Aurifeuillean factorization

In number theory, an aurifeuillean factorization, named after Léon-François-Antoine Aurifeuille, is a special type of algebraic factorization that comes from non-trivial factorizations of cyclotomic polynomials over the integers.^[1] Although cyclotomic polynomials themselves are irreducible over the integers, when restricted to particular integer values they may have an algebraic factorization, as in the examples below.

Examples

Numbers of the form 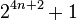$2^{4n+2}+1$ have the following aurifeuillean factorization:^[2]

2^{4n+2}+1 = (2^{2n+1}-2^{n+1}+1)\cdot (2^{2n+1}+2^{n+1}+1).

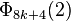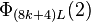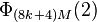As so, when k is a natural number > 1, $\Phi_{8k+4}(2)$ cannot be a prime, so there are two factors, $\Phi_{(8k+4)L}(2)$ and $\Phi_{(8k+4)M}(2)$ , for example, 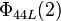$\Phi_{44L}(2)$ = 397, and 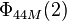$\Phi_{44M}(2)$ = 2113.

Numbers of the form 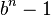$b^n - 1$ , where 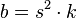$b = s^2\cdot k$ with square-free 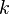$k$ , have aurifeuillean factorization if one of the following conditions holds:
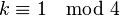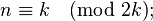
(i) $k\equiv 1 \mod 4$ and $n\equiv k \pmod{2k};$

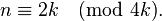
(ii) $k\equiv 2, 3 \pmod 4$ and $n\equiv 2k \pmod{4k}.$

Numbers of the form 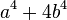$a^4 + 4b^4$ have the following aurifeuillean factorization:

a^4 + 4b^4 = (a^2 - 2ab + 2b^2)\cdot (a^2 + 2ab + 2b^2).

Lucas number 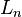$L_n$ , when n congruent to 5 (mod 10), have the following aurifeuillean factorization:

L_{5n} = (5F_n^2-5F_n+1)(5F_n^2+5F_n+1)

k-Lucas number, or (k, -1)-Lucas number, let k² + 4 = a² * b with squarefree b, when n congruent to b (mod 2b) also have aurifeuillian factorization.

History

In 1871, Aurifeuille discovered the factorization of 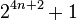$2^{4n+2}+1$ for n = 14 as the following:^[2]^[3]

2^{58}+1 = 536838145 \cdot 536903681. \,\!

The second factor is prime, and the factorization of the first factor is 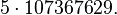$5 \cdot 107367629.$ ^[3] The general form of the factorization was later discovered by Lucas.^[2]

References

↑ A. Granville, P. Pleasants (2006). "Aurifeuillian factorization". Math. Comp. 75: 497–508. doi:10.1090/S0025-5718-05-01766-7.
↑ 2.0 2.1 2.2 Weisstein, Eric W., "Aurifeuillean Factorization", MathWorld.
↑ 3.0 3.1 Integer Arithmetic, Number Theory – Aurifeuillian Factorizations, Numericana

External links

Aurifeuillian Factorisation, Colin Barker