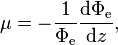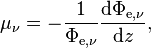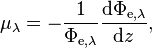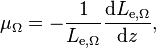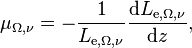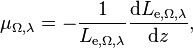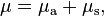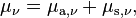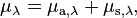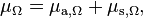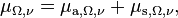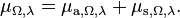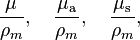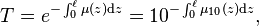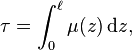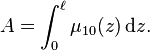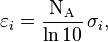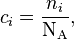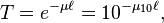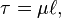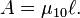Attenuation coefficient

For "attenuation coefficient" as it applies to electromagnetic theory and telecommunications see propagation constant. For the "mass attenuation coefficient", see the article mass attenuation coefficient.

Attenuation coefficient or narrow beam attenuation coefficient of the volume of a material characterizes how easily it can be penetrated by a beam of light, sound, particles, or other energy or matter.^[1] A large attenuation coefficient means that the beam is quickly "attenuated" (weakened) as it passes through the medium, and a small attenuation coefficient means that the medium is relatively transparent to the beam. The SI unit of attenuation coefficient is the reciprocal metre (m⁻¹). "Extinction coefficient" is an old term for this quantity.^[1]

Overview

Attenuation coefficient describes the extent to which the radiant flux of a beam is reduced as it passes through a specific material. It is used in the context of:

X-rays or Gamma rays, where it is denoted μ and measured in cm⁻¹;
neutrons and nuclear reactors, where it is called macroscopic cross section (although actually it is not a section dimensionally speaking), denoted Σ and measured in m⁻¹;
solar and infrared radiative transfer in the atmosphere, albeit usually denoted with another symbol (given the standard use of μ = cos θ for slant paths);
ultrasound attenuation, where it is denoted α and measured in dB·cm⁻¹·MHz⁻¹;^[2]^[3]
acoustics for characterizing particle size distribution, where it is denoted α and measured in m⁻¹.

A small attenuation coefficient indicates that the material in question is relatively transparent, while a larger value indicates greater degrees of opacity. The attenuation coefficient is dependent upon the type of material and the energy of the radiation. Generally, for electromagnetic radiation, the higher the energy of the incident photons and the less dense the material in question, the lower the corresponding attenuation coefficient will be.

Mathematical definitions

Hemispherical attenuation coefficient

Hemispherical attenuation coefficient of a volume, denoted μ, is defined as^[4]

\mu = -\frac{1}{\Phi_\mathrm{e}} \frac{\mathrm{d}\Phi_\mathrm{e}}{\mathrm{d}z},

where

Φ_e is the radiant flux;
z is the path length of the beam.

Spectral hemispherical attenuation coefficient

Spectral hemispherical attenuation coefficient in frequency and spectral hemispherical attenuation coefficient in wavelength of a volume, denoted μ_ν and μ_λ respectively, are defined as^[4]

\mu_\nu = -\frac{1}{\Phi_{\mathrm{e},\nu}} \frac{\mathrm{d}\Phi_{\mathrm{e},\nu}}{\mathrm{d}z},

\mu_\lambda = -\frac{1}{\Phi_{\mathrm{e},\lambda}} \frac{\mathrm{d}\Phi_{\mathrm{e},\lambda}}{\mathrm{d}z},

where

Φ_e,ν is the spectral radiant flux in frequency;
Φ_e,λ is the spectral radiant flux in wavelength.

Directional attenuation coefficient

Directional attenuation coefficient of a volume, denoted μ_Ω, is defined as^[4]

\mu_\Omega = -\frac{1}{L_{\mathrm{e},\Omega}} \frac{\mathrm{d}L_{\mathrm{e},\Omega}}{\mathrm{d}z},

where L_e,Ω is the radiance.

Spectral directional attenuation coefficient

Spectral directional attenuation coefficient in frequency and spectral directional attenuation coefficient in wavelength of a volume, denoted μ_Ω,ν and μ_Ω,λ respectively, are defined as^[4]

\mu_{\Omega,\nu} = -\frac{1}{L_{\mathrm{e},\Omega,\nu}} \frac{\mathrm{d}L_{\mathrm{e},\Omega,\nu}}{\mathrm{d}z},

\mu_{\Omega,\lambda} = -\frac{1}{L_{\mathrm{e},\Omega,\lambda}} \frac{\mathrm{d}L_{\mathrm{e},\Omega,\lambda}}{\mathrm{d}z},

where

L_e,Ω,ν is the spectral radiance in frequency;
L_e,Ω,λ is the spectral radiance in wavelength.

Absorption and scattering coefficients

When a narrow (collimated) beam passes through a volume, the beam will lose intensity due to two processes: absorption and scattering.

Absorption coefficient of a volume, denoted μ_a, and scattering coefficient of a volume, denoted μ_s, are defined the same way as for attenuation coefficient.^[4]

Attenuation coefficient of a volume is the sum of absorption coefficient and scattering coefficient:^[4]

\mu = \mu_\mathrm{a} + \mu_\mathrm{s},

\mu_\nu = \mu_{\mathrm{a},\nu} + \mu_{\mathrm{s},\nu},

\mu_\lambda = \mu_{\mathrm{a},\lambda} + \mu_{\mathrm{s},\lambda},

\mu_\Omega = \mu_{\mathrm{a},\Omega} + \mu_{\mathrm{s},\Omega},

\mu_{\Omega,\nu} = \mu_{\mathrm{a},\Omega,\nu} + \mu_{\mathrm{s},\Omega,\nu},

\mu_{\Omega,\lambda} = \mu_{\mathrm{a},\Omega,\lambda} + \mu_{\mathrm{s},\Omega,\lambda}.

Just looking at the narrow beam itself, the two processes cannot be distinguished. However, if a detector is set up to measure beam leaving in different directions, or conversely using a non-narrow beam, one can measure how much of the lost radiant flux was scattered, and how much was absorbed.

In this context, the "absorption coefficient" measures how quickly the beam would lose radiant flux due to the absorption alone, while "attenuation coefficient" measures the total loss of narrow-beam intensity, including scattering as well. "Narrow-beam attenuation coefficient" always unambiguously refers to the latter. The attenuation coefficient is always larger than the absorption coefficient, although they are equal in the idealized case of no scattering.

Mass attenuation, absorption, and scattering coefficients

Main article: Mass attenuation coefficient

Mass attenuation coefficient, mass absorption coefficient, and mass scattering coefficient are defined as^[4]

\frac{\mu}{\rho_m},\quad \frac{\mu_\mathrm{a}}{\rho_m},\quad \frac{\mu_\mathrm{s}}{\rho_m},

where ρ_m is the mass density.

Beer–Lambert law

Main article: Beer–Lambert law

The radiant flux transmitted through a layer of material with thickness ℓ is related to the incident radiant flux according to the inverse exponential power law that, for light, is usually referred to as Beer–Lambert law:

T = e^{-\int_0^\ell \mu(z)\mathrm{d}z} = 10^{-\int_0^\ell \mu_{10}(z)\mathrm{d}z},

or equivalently that

\tau = \int_0^\ell \mu(z)\,\mathrm{d}z,

A = \int_0^\ell \mu_{10}(z)\,\mathrm{d}z.

where

σ_i is the attenuation cross section of the attenuating specie i in the material sample;
n_i is the number density of the attenuating specie i in the material sample;
ε_i is the molar attenuation coefficient of the attenuating specie i in the material sample;
c_i is the amount concentration of the attenuating specie i in the material sample;
ℓ is the path length of the beam of light through the material sample.

Attenuation cross section and molar attenuation coefficient are related by

\varepsilon_i = \frac{\mathrm{N_A}}{\ln{10}}\,\sigma_i,

and number density and amount concentration by

c_i = \frac{n_i}{\mathrm{N_A}},

where N_A is the Avogadro constant.

In case of uniform attenuation, these relations become

T = e^{-\mu\ell} = 10^{-\mu_{10}\ell},

or equivalently

\tau = \mu\ell,

A = \mu_{10}\ell.

Cases of non-uniform attenuation occur in atmospheric science applications and radiation shielding theory for instance.

The half-value layer (HVL) is the thickness of a layer of material required to reduce the radiant flux of the transmitted radiation to half its incident magnitude. The half-value layer is about 69% (ln 2) of the penetration depth. It is from these equations that engineers decide how much protection is needed for "safety" from potentially harmful radiation. The attenuation factor of a material is obtained by the ratio of the transmitted to the incident radiation radiant fluxes Φ_e^t/Φ_eⁱ.

Attenuation coefficient is also inversely related to mean free path. Moreover, it is very closely related to the attenuation cross section.

SI radiometry units

**SI Radiometry Quantities**
Quantity		Unit		Dimension	Notes
Name	Symbol^{[nb 1]}	Name	Symbol	Symbol	Notes
Radiant energy	Q_e^{[nb 2]}	joule	J	M⋅L²⋅T⁻²	Energy of electromagnetic radiation.
Radiant energy density	w_e	joule per cubic metre	J/m³	M⋅L⁻¹⋅T⁻²	Radiant energy per unit volume.
Radiant flux	Φ_e^{[nb 2]}	watt	W or J/s	M⋅L²⋅T⁻³	Radiant energy emitted, reflected, transmitted or received, per unit time. This is sometimes also called "radiant power".
Spectral flux	Φ_e,ν^{[nb 3]} or Φ_e,λ^{[nb 4]}	watt per hertz or watt per metre	W/Hz or W/m	M⋅L²⋅T⁻² or M⋅L⋅T⁻³	Radiant flux per unit frequency or wavelength. The latter is commonly measured in W⋅sr⁻¹⋅m⁻²⋅nm⁻¹.
Radiant intensity	I_e,Ω^{[nb 5]}	watt per steradian	W/sr	M⋅L²⋅T⁻³	Radiant flux emitted, reflected, transmitted or received, per unit solid angle. This is a directional quantity.
Spectral intensity	I_e,Ω,ν^{[nb 3]} or I_e,Ω,λ^{[nb 4]}	watt per steradian per hertz or watt per steradian per metre	W⋅sr⁻¹⋅Hz⁻¹ or W⋅sr⁻¹⋅m⁻¹	M⋅L²⋅T⁻² or M⋅L⋅T⁻³	Radiant intensity per unit frequency or wavelength. The latter is commonly measured in W⋅sr⁻¹⋅m⁻²⋅nm⁻¹. This is a directional quantity.
Radiance	L_e,Ω^{[nb 5]}	watt per steradian per square metre	W⋅sr⁻¹⋅m⁻²	M⋅T⁻³	Radiant flux emitted, reflected, transmitted or received by a surface, per unit solid angle per unit projected area. This is a directional quantity. This is sometimes also confusingly called "intensity".
Spectral radiance	L_e,Ω,ν^{[nb 3]} or L_e,Ω,λ^{[nb 4]}	watt per steradian per square metre per hertz or watt per steradian per square metre, per metre	W⋅sr⁻¹⋅m⁻²⋅Hz⁻¹ or W⋅sr⁻¹⋅m⁻³	M⋅T⁻² or M⋅L⁻¹⋅T⁻³	Radiance of a surface per unit frequency or wavelength. The latter is commonly measured in W⋅sr⁻¹⋅m⁻²⋅nm⁻¹. This is a directional quantity. This is sometimes also confusingly called "spectral intensity".
Irradiance	E_e^{[nb 2]}	watt per square metre	W/m²	M⋅T⁻³	Radiant flux received by a surface per unit area. This is sometimes also confusingly called "intensity".
Spectral irradiance	E_e,ν^{[nb 3]} or E_e,λ^{[nb 4]}	watt per square metre per hertz or watt per square metre, per metre	W⋅m⁻²⋅Hz⁻¹ or W/m³	M⋅T⁻² or M⋅L⁻¹⋅T⁻³	Irradiance of a surface per unit frequency or wavelength. The former is commonly measured in 10⁻²² W⋅m⁻²⋅Hz⁻¹, known as solar flux unit, and the latter in W⋅m⁻²⋅nm⁻¹.^{[nb 6]} This is sometimes also confusingly called "spectral intensity".
Radiosity	J_e^{[nb 2]}	watt per square metre	W/m²	M⋅T⁻³	Radiant flux leaving (emitted, reflected and transmitted by) a surface per unit area. This is sometimes also confusingly called "intensity".
Spectral radiosity	J_e,ν^{[nb 3]} or J_e,λ^{[nb 4]}	watt per square metre per hertz or watt per square metre, per metre	W⋅m⁻²⋅Hz⁻¹ or W/m³	M⋅T⁻² or M⋅L⁻¹⋅T⁻³	Radiosity of a surface per unit frequency or wavelength. The latter is commonly measured in W⋅m⁻²⋅nm⁻¹. This is sometimes also confusingly called "spectral intensity".
Radiant exitance	M_e^{[nb 2]}	watt per square metre	W/m²	M⋅T⁻³	Radiant flux emitted by a surface per unit area. This is the emitted component of radiosity. "Radiant emittance" is an old term for this quantity. This is sometimes also confusingly called "intensity".
Spectral exitance	M_e,ν^{[nb 3]} or M_e,λ^{[nb 4]}	watt per square metre per hertz or watt per square metre, per metre	W⋅m⁻²⋅Hz⁻¹ or W/m³	M⋅T⁻² or M⋅L⁻¹⋅T⁻³	Radiant exitance of a surface per unit frequency or wavelength. The latter is commonly measured in W⋅m⁻²⋅nm⁻¹. "Spectral emittance" is an old term for this quantity. This is sometimes also confusingly called "spectral intensity".
Radiant exposure	H_e	joule per square metre	J/m²	M⋅T⁻²	Radiant energy received by a surface per unit area, or equivalently irradiance of a surface integrated over time of irradiation. This is sometimes also called "radiant fluence".
Spectral exposure	H_e,ν^{[nb 3]} or H_e,λ^{[nb 4]}	joule per square metre per hertz or joule per square metre, per metre	J⋅m⁻²⋅Hz⁻¹ or J/m³	M⋅T⁻¹ or M⋅L⁻¹⋅T⁻²	Radiant exposure of a surface per unit frequency or wavelength. The latter is commonly measured in J⋅m⁻²⋅nm⁻¹. This is sometimes also called "spectral fluence".
Hemispherical emissivity	ε			1	Radiant exitance of a surface, divided by that of a black body at the same temperature as that surface.
Spectral hemispherical emissivity	ε_ν or ε_λ			1	Spectral exitance of a surface, divided by that of a black body at the same temperature as that surface.
Directional emissivity	ε_Ω			1	Radiance emitted by a surface, divided by that emitted by a black body at the same temperature as that surface.
Spectral directional emissivity	ε_Ω,ν or ε_Ω,λ			1	Spectral radiance emitted by a surface, divided by that of a black body at the same temperature as that surface.
Hemispherical absorptance	A			1	Radiant flux absorbed by a surface, divided by that received by that surface. This should not be confused with "absorbance".
Spectral hemispherical absorptance	A_ν or A_λ			1	Spectral flux absorbed by a surface, divided by that received by that surface. This should not be confused with "spectral absorbance".
Directional absorptance	A_Ω			1	Radiance absorbed by a surface, divided by the radiance incident onto that surface. This should not be confused with "absorbance".
Spectral directional absorptance	A_Ω,ν or A_Ω,λ			1	Spectral radiance absorbed by a surface, divided by the spectral radiance incident onto that surface. This should not be confused with "spectral absorbance".
Hemispherical reflectance	R			1	Radiant flux reflected by a surface, divided by that received by that surface.
Spectral hemispherical reflectance	R_ν or R_λ			1	Spectral flux reflected by a surface, divided by that received by that surface.
Directional reflectance	R_Ω			1	Radiance reflected by a surface, divided by that received by that surface.
Spectral directional reflectance	R_Ω,ν or R_Ω,λ			1	Spectral radiance reflected by a surface, divided by that received by that surface.
Hemispherical transmittance	T			1	Radiant flux transmitted by a surface, divided by that received by that surface.
Spectral hemispherical transmittance	T_ν or T_λ			1	Spectral flux transmitted by a surface, divided by that received by that surface.
Directional transmittance	T_Ω			1	Radiance transmitted by a surface, divided by that received by that surface.
Spectral directional transmittance	T_Ω,ν or T_Ω,λ			1	Spectral radiance transmitted by a surface, divided by that received by that surface.
Hemispherical attenuation coefficient	μ	reciprocal metre	m⁻¹	L⁻¹	Radiant flux absorbed and scattered by a volume per unit length, divided by that received by that volume.
Spectral hemispherical attenuation coefficient	μ_ν or μ_λ	reciprocal metre	m⁻¹	L⁻¹	Spectral radiant flux absorbed and scattered by a volume per unit length, divided by that received by that volume.
Directional attenuation coefficient	μ_Ω	reciprocal metre	m⁻¹	L⁻¹	Radiance absorbed and scattered by a volume per unit length, divided by that received by that volume.
Spectral directional attenuation coefficient	μ_Ω,ν or μ_Ω,λ	reciprocal metre	m⁻¹	L⁻¹	Spectral radiance absorbed and scattered by a volume per unit length, divided by that received by that volume.
See also: SI · Radiometry · Photometry

↑ Standards organizations recommend that radiometric quantities should be denoted with suffix "e" (for "energetic") to avoid confusion with photometric or photon quantities.
↑ 2.0 2.1 2.2 2.3 2.4 Alternative symbols sometimes seen: W or E for radiant energy, P or F for radiant flux, I for irradiance, W for radiant exitance.
↑ 3.0 3.1 3.2 3.3 3.4 3.5 3.6 Spectral quantities given per unit frequency are denoted with suffix "ν" (Greek)—not to be confused with suffix "v" (for "visual") indicating a photometric quantity.
↑ 4.0 4.1 4.2 4.3 4.4 4.5 4.6 Spectral quantities given per unit wavelength are denoted with suffix "λ" (Greek).
↑ 5.0 5.1 Directional quantities are denoted with suffix "Ω" (Greek).
↑ NOAA / Space Weather Prediction Center includes a definition of the solar flux unit (SFU).

References

↑ 1.0 1.1 IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "Attenuation coefficient".
↑ ISO 20998-1:2006 "Measurement and characterization of particles by acoustic methods"
↑ Dukhin, A.S. and Goetz, P.J. "Ultrasound for characterizing colloids", Elsevier, 2002
↑ 4.0 4.1 4.2 4.3 4.4 4.5 4.6 "Thermal insulation — Heat transfer by radiation — Physical quantities and definitions". ISO 9288:1989. ISO catalogue. 1989. Retrieved 2015-03-15.

Attenuation coefficient

Overview

Mathematical definitions

Hemispherical attenuation coefficient

Spectral hemispherical attenuation coefficient

Directional attenuation coefficient

Spectral directional attenuation coefficient

Absorption and scattering coefficients

Mass attenuation, absorption, and scattering coefficients

Beer–Lambert law

SI radiometry units

See also

References

External links