Atoroidal
In mathematics, an atoroidal 3-manifold is one that does not contain an essential torus.
There are two major variations in this terminology: a torus may be defined geometrically, as an embedded, non-boundary parallel, incompressible torus, or it may be defined algebraically, as a subgroup 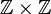 of its fundamental group that is not conjugate to a peripheral subgroup (i.e. the image of the map on fundamental group induced by an inclusion of a boundary component). The terminology is not standardized, and different authors require atoroidal 3-manifolds to satisfy certain additional restrictions. For instance:
of its fundamental group that is not conjugate to a peripheral subgroup (i.e. the image of the map on fundamental group induced by an inclusion of a boundary component). The terminology is not standardized, and different authors require atoroidal 3-manifolds to satisfy certain additional restrictions. For instance:
- Apanasov (2000) gives a definition of atoroidality that combines both geometric and algebraic aspects, in terms of maps from a torus to the manifold and the induced maps on the fundamental group. He then notes that for irreducible boundary-incompressible 3-manifolds this gives the algebraic definition.[1]
- Otal (2001) uses the algebraic definition without additional restrictions.[2]
- Chow (2007) uses the geometric definition, restricted to irreducible manifolds.[3]
- Kapovich (2009) requires the algebraic variant of atoroidal manifolds (which he calls simply atoroidal) to avoid being one of three kinds of fiber bundle. He makes the same restriction on geometrically atoroidal manifolds (which he calls topologically atoroidal) and in addition requires them to avoid incompressible boundary-parallel embedded Klein bottles. With these definitions, the two kinds of atoroidality are equivalent except on certain Seifert manifolds.[4]
A 3-manifold that is not atoroidal is called toroidal.
References
- ↑ Apanasov, Boris N. (2000), Conformal Geometry of Discrete Groups and Manifolds, De Gruyter Expositions in Mathematics 32, Walter de Gruyter, p. 294, ISBN 9783110808056.
- ↑ Otal, Jean-Pierre (2001), The Hyperbolization Theorem for Fibered 3-manifolds, Contemporary Mathematics 7, American Mathematical Society, p. ix, ISBN 9780821821534.
- ↑ Chow, Bennett (2007), The Ricci Flow: Geometric aspects, Mathematical surveys and monographs, American Mathematical Society, p. 436, ISBN 9780821839461.
- ↑ Kapovich, Michael (2009), Hyperbolic Manifolds and Discrete Groups, Progress in Mathematics 183, Springer, p. 6, ISBN 9780817649135.