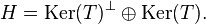Atkinson's theorem
In operator theory, Atkinson's theorem (named for Frederick Valentine Atkinson) gives a characterization of Fredholm operators.
The theorem
Let H be a Hilbert space and L(H) the set of bounded operators on H. The following is the classical definition of a Fredholm operator: an operator T ∈ L(H) is said to be a Fredholm operator if the kernel Ker(T) is finite-dimensional, Ker(T*) is finite-dimensional (where T* denotes the adjoint of T), and the range Ran(T) is closed.
Atkinson's theorem states:
- A T ∈ L(H) is a Fredholm operator if and only if T is invertible modulo compact perturbation, i.e. TS = I + C1 and ST = I + C2 for some bounded operator S and compact operators C1 and C2.
In other words, an operator T ∈ L(H) is Fredholm, in the classical sense, if and only if its projection in the Calkin algebra is invertible.
Sketch of proof
The outline of a proof is as follows. For the ⇒ implication, express H as the orthogonal direct sum
The restriction T : Ker(T)⊥ → Ran(T) is a bijection, and therefore invertible by the open mapping theorem. Extend this inverse by 0 on Ran(T)⊥ = Ker(T*) to an operator S defined on all of H. Then I − TS is the finite-rank projection onto Ker(T*), and I − ST is the projection onto Ker(T). This proves the only if part of the theorem.
For the converse, suppose now that ST = I + C2 for some compact operator C2. If x ∈ Ker(T), then STx = x + C2x = 0. So Ker(T) is contained in an eigenspace of C2, which is finite-dimensional (see spectral theory of compact operators). Therefore Ker(T) is also finite-dimensional. The same argument shows that Ker(T*) is also finite-dimensional.
To prove that Ran(T) is closed, we make use of the approximation property: let F be a finite-rank operator such that ||F − C2|| < r. Then for every x in Ker(F),
- ||S||·||Tx|| ≥ ||STx|| = ||x + C2x|| = ||x + Fx +C2x − Fx|| ≥ ||x|| − ||C2 − F||·||x|| ≥ (1 − r)||x||.
Thus T is bounded below on Ker(F), which implies that T(Ker(F)) is closed. On the other hand, T(Ker(F)⊥) is finite-dimensional, since Ker(F)⊥ = Ran(F*) is finite-dimensional. Therefore Ran(T) = T(Ker(F)) + T(Ker(F)⊥) is closed, and this proves the theorem.
References
- Atkinson, F. V. (1951). "The normal solvability of linear equations in normed spaces". Mat. Sb. 28 (70): 3–14. Zbl 0042.12001.