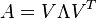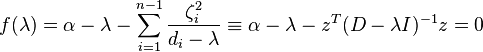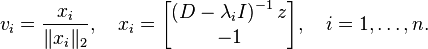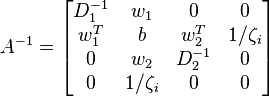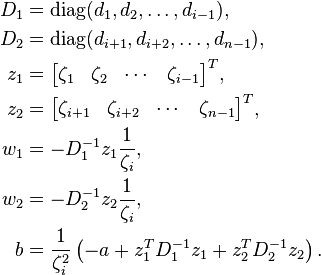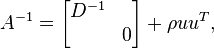Arrowhead matrix

In the mathematical field of linear algebra, an arrowhead matrix is a square matrix containing zeros in all entries except for the first row, first column, and main diagonal.^[1] ^[2] In other words, the matrix has the form

A=\begin{bmatrix} \,\! *&*&*&*&* \\ \,\! *&*&0&0&0 \\ \,\! *&0&*&0&0 \\ \,\! *&0&0&*&0 \\ \,\! *&0&0&0&* \end{bmatrix}.

Any symmetric permutation of the arrowhead matrix, 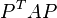$P^T A P$ , where P is a permutation matrix, is a (permuted) arrowhead matrix. Real symmetric arrowhead matrices are used in some algorithms for finding of eigenvalues and eigenvectors.^[3]

Real symmetric arrowhead matrices

Let A be a real symmetric (permuted) arrowhead matrix of the form

A=\left[ \begin{array}{cc} D & z \\ z^{T} & \alpha \end{array} \right],

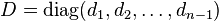where $D=\mathop{\mathrm{diag}}(d_{1},d_{2},\ldots ,d_{n-1})$ is diagonal matrix of order n-1, 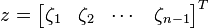$z=\begin{bmatrix} \zeta _{1} & \zeta _{2} & \cdots & \zeta _{n-1} \end{bmatrix}^T$ is a vector and 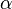$\alpha$ is a scalar. Let

A=V\Lambda V^{T}

be the eigenvalue decomposition of A, where 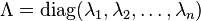$\Lambda =\mathop{\mathrm{diag}}(\lambda_1,\lambda_2,\ldots ,\lambda_n)$ is a diagonal matrix whose diagonal elements are the eigenvalues of A, and 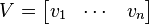$V=\begin{bmatrix}v_{1} & \cdots & v_{n} \end{bmatrix}$ is an orthonormal matrix whose columns are the corresponding eigenvectors. The following holds:

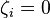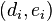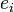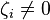If $\zeta_i=0$ for some i, then the pair $(d_i,e_i)$ , where $e_i$ is the i-th standard basis vector, is an eigenpair of A. Thus, all such rows and columns can be deleted, leaving the matrix with all $\zeta_i\neq 0$ .
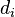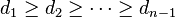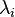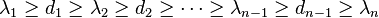The Cauchy interlacing theorem implies that the sorted eigenvalues of A interlace the sorted elements $d_i$ : if $d_1 \geq d_2\geq \cdots\geq d_{n-1}$ (this can be attained by symmetric permutation of rows and columns without loss of generality), and if $\lambda_i$ s are sorted accordingly, then $\lambda_1\geq d_1\geq \lambda_2\geq d_2\geq \cdots \geq \lambda_{n-1} \geq d_{n-1} \geq \lambda_n$ .
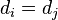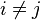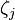If $d_i=d_j$ , for some $i\neq j$ , the above inequality implies that $d_{i}$ is an eigenvalue of A. The size of the problem can be reduced by annihilating $\zeta_j$ with a Givens rotation in the 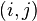$(i,j)$ -plane and proceeding as above.

Eigenvalues and eigenvectors

Symmetric arrowhead matrix is irreducible if 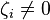$\zeta_i\neq 0$ for all i and 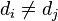$d_{i}\neq d_{j}$ for all 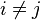$i\neq j$ . The eigenvalues of an irreducible real symmetric arrowhead matrix are the zeros of the secular equation

f(\lambda )=\alpha -\lambda -\sum_{i=1}^{n-1}\frac{\zeta _{i}^{2}}{ d_{i}-\lambda }\equiv \alpha -\lambda -z^{T}(D-\lambda I)^{-1}z=0

which can be, for example, computed by the bisection method. The corresponding eigenvectors are equal to

v_{i}=\frac{x_{i}}{\| x_{i}\| _{2}}, \quad x_{i}= \begin{bmatrix} \left( D-\lambda _{i}I\right)^{-1}z \\ -1 \end{bmatrix}, \quad i=1,\ldots ,n.

Direct application of the above formula may yield eigenvectors which are not numerically sufficiently orthogonal.^[1] The forward stable algorithm which computes each eigenvalue and each component of the corresponding eigenvector to almost full accuracy is described in.^[2] The Julia version of the software is available.^[4]

Inverses

Let A be an irreducible real symmetric arrowhead matrix. If 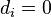$d_i=0$ for some i, the inverse is a permuted irreducible real symmetric arrowhead matrix:

A^{-1}=\begin{bmatrix} D_{1}^{-1} & w_{1} & 0 & 0 \\ w_{1}^{T} & b & w_{2}^{T} & 1/\zeta _{i} \\ 0 & w_{2} & D_{2}^{-1} & 0 \\ 0 & 1/\zeta _{i} & 0 & 0 \end{bmatrix}

where

\begin{alignat}{2} D_1& =\mathop{\mathrm{diag}}(d_{1},d_{2},\ldots ,d_{i-1}), \\ D_2&=\mathop{\mathrm{diag}}(d_{i+1},d_{i+2},\ldots ,d_{n-1}),\\ z_1&=\begin{bmatrix} \zeta _{1} & \zeta _{2} & \cdots & \zeta _{i-1}\end{bmatrix}^T, \\ z_2&=\begin{bmatrix} \zeta _{i+1} & \zeta _{i+2} & \cdots & \zeta _{n-1}\end{bmatrix}^T,\\ w_{1}&=-D_{1}^{-1}z_{1}\frac{1}{\zeta _{i}},\\ w_{2}&=-D_{2}^{-1}z_{2}\frac{1}{\zeta _{i}},\\ b&=\frac{1}{\zeta _{i}^{2}}\left( -a+z_{1}^{T}D_{1}^{-1}z_{1}+z_{2}^{T}D_{2}^{-1}z_{2}\right). \end{alignat}

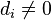If $d_i\neq 0$ for all i, the inverse is a rank-one modification of a diagonal matrix (diagonal-plus-rank-one matrix or DPR1):

A^{-1}=\begin{bmatrix} D^{-1} & \\ & 0\end{bmatrix}+\rho uu^{T},

where

u=\begin{bmatrix} D^{-1} z \\ -1\end{bmatrix},\quad \rho =\frac{1}{\alpha-z^{T}D^{-1}z}.

References

↑ 1.0 1.1 O'Leary, D. P.; Stewart, G. W. (1990). "Computing the eigenvalues and eigenvectors of symmetric arrowhead matrices". Journal of Computational Physics 90: 497–505. doi:10.1016/0021-9991(90)90177-3.
↑ 2.0 2.1 Jakovcevic Stor, Nevena; Slapnicar, Ivan; Barlow, Jesse L. (2015). "Accurate eigenvalue decomposition of real symmetric arrowhead matrices and applications". Linear Algebra and Its Applications 464: 62–89. arXiv:1302.7203. doi:10.1016/j.laa.2013.10.007.
↑ Gu, Ming; Eisenstat, Stanley C. (1995). "A Divide-and-Conquer Algorithm for the Symmetric Tridiagonal Eigenproblem". SIAM Journal on Matrix Analysis and Applications 16: 172. doi:10.1137/S0895479892241287.
↑ "Arrowhead.jl"