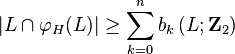Arnold–Givental conjecture

The Arnold–Givental conjecture, named after Vladimir Arnold and Alexander Givental, is a statement on Lagrangian submanifolds. It gives a lower bound in terms of the Betti numbers of $L$ on the number of intersection points of $L$ with a Hamiltonian isotopic Lagrangian submanifold which intersects $L$ transversally.

Let $H t \in C \infty (M); 0 \leq t \leq 1$ be a smooth family of Hamiltonian functions of $M$ and denote by $φ H$ the one-time map of the flow of the Hamiltonian vector field $X H t$ of $H t$ . Assume that $L$ and $φ H (L)$ intersect transversally. Then the number of intersection points of $L$ and $φ H (L)$ can be estimated from below by the sum of the $Z 2$ Betti numbers of $L$ , i.e.

\left | L \cap \varphi_H (L) \right | \geq \sum_{k=0}^n b_k \left (L; \mathbf{Z}_2 \right)

Up to now, the Arnold–Givental conjecture could only be proven under some additional assumptions.

References

Frauenfelder, Urs (2004), "The Arnold–Givental conjecture and moment Floer homology", International Mathematics Research Notices (42): 2179–2269, doi:10.1155/S1073792804133941, MR 2076142 .
Oh, Yong-Geun (1992), "Floer cohomology and Arnol'd-Givental's conjecture of [on] Lagrangian intersections", Comptes Rendus de l'Académie des Sciences 315 (3): 309–314, MR 1179726 .

Arnold–Givental conjecture

See also

References