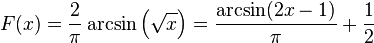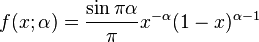Arcsine distribution
|
Probability density function
| |
|
Cumulative distribution function
| |
| Parameters | none |
|---|---|
| Support |
![x \in [0,1]](../I/m/c628ba2b1047de93f66cb815d986e107.png) |
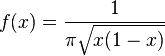 | |
| CDF |
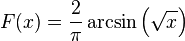 |
| Mean |
 |
| Median |
 |
| Mode |
 |
| Variance |
 |
| Skewness |
 |
| Ex. kurtosis |
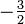 |
| Entropy |
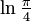 |
| MGF |
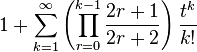 |
| CF |
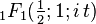 |
In probability theory, the arcsine distribution is the probability distribution whose cumulative distribution function is
for 0 ≤ x ≤ 1, and whose probability density function is
on (0, 1). The standard arcsine distribution is a special case of the beta distribution with α = β = 1/2. That is, if  is the standard arcsine distribution then
is the standard arcsine distribution then 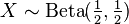
The arcsine distribution appears
- in the Lévy arcsine law;
- in the Erdős arcsine law;
- as the Jeffreys prior for the probability of success of a Bernoulli trial.
Generalization
| Parameters |
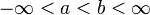 |
|---|---|
| Support |
![x \in [a,b]](../I/m/8290bddba5acf9822dcbf61f4ac67d1b.png) |
 | |
| CDF |
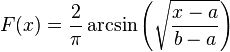 |
| Mean |
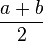 |
| Median |
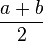 |
| Mode |
 |
| Variance |
 |
| Skewness |
 |
| Ex. kurtosis |
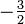 |
Arbitrary bounded support
The distribution can be expanded to include any bounded support from a ≤ x ≤ b by a simple transformation
for a ≤ x ≤ b, and whose probability density function is
on (a, b).
Shape factor
The generalized standard arcsine distribution on (0,1) with probability density function
is also a special case of the beta distribution with parameters 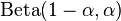 .
.
Note that when 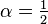 the general arcsine distribution reduces to the standard distribution listed above.
the general arcsine distribution reduces to the standard distribution listed above.
Properties
- Arcsine distribution is closed under translation and scaling by a positive factor
- If
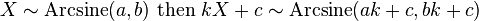
- If
- The square of an arc sine distribution over (-1, 1) has arc sine distribution over (0, 1)
- If

- If
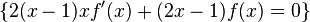
Related distributions
- If U and V are i.i.d uniform (−π,π) random variables, then
 ,
, 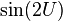 ,
, 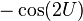 ,
, 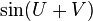 and
and 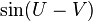 all have an
all have an  distribution.
distribution. - If
 is the generalized arcsine distribution with shape parameter
is the generalized arcsine distribution with shape parameter  supported on the finite interval [a,b] then
supported on the finite interval [a,b] then 
See also
- Arcsine
References
- Rogozin, B.A. (2001), "A/a013160", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
| ||||||||||||||