Approximation property

The construction of a Banach space without the approximation property earned Per Enflo a live goose in 1972, which had been promised by Stanisław Mazur (left) in 1936.

In mathematics, a Banach space is said to have the approximation property (AP), if every compact operator is a limit of finite-rank operators. The converse is always true.

Every Hilbert space has this property. There are, however, Banach spaces which do not; Per Enflo published the first counterexample in a 1973 article. However, a lot of work in this area was done by Grothendieck (1955).

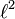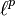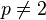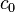Later many other counterexamples were found. The space of bounded operators on $\ell^2$ does not have the approximation property (Szankowski). The spaces $\ell^p$ for $p\neq 2$ and $c_0$ (see Sequence space) have closed subspaces that do not have the approximation property.

Definition

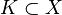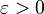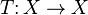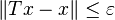A locally convex topological vector space $X$ is said to have the approximation property, if the identity map can be approximated, uniformly on precompact sets, by continuous linear maps of finite rank.^[1] If X is a Banach space the this requirement becomes that for every compact set $K\subset X$ and every $\varepsilon>0$ , there is an operator $T\colon X\to X$ of finite rank so that $\|Tx-x\|\leq\varepsilon$ , for every $x \in K$ .

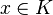Some other flavours of the AP are studied:

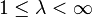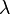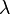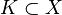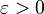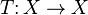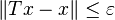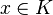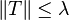Let $X$ be a Banach space and let $1\leq\lambda<\infty$ . We say that X has the $\lambda$ -approximation property ( $\lambda$ -AP), if, for every compact set $K\subset X$ and every $\varepsilon>0$ , there is an operator $T\colon X \to X$ of finite rank so that $\|Tx - x\|\leq\varepsilon$ , for every $x \in K$ , and $\|T\|\leq\lambda$ .

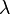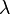A Banach space is said to have bounded approximation property (BAP), if it has the $\lambda$ -AP for some $\lambda$ .

A Banach space is said to have metric approximation property (MAP), if it is 1-AP.

A Banach space is said to have compact approximation property (CAP), if in the definition of AP an operator of finite rank is replaced with a compact operator.

Examples

Every projective limit of Hilbert spaces, as well as any subspace of such a projective limit, possesses the approximation property.^[2]
- Hence every nuclear space possesses the approximation property.
Every subspace of an arbitrary product of Hilbert spaces possesses the approximation property.^[3]
Every separable Frechet space that contains a Schauder basis possesses the approximation property.^[4]
Every space with a Schauder basis has the AP (we can use the projections associated to the base as the 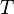$T$ 's in the definition), thus a lot of spaces with the AP can be found. For example, the 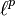$\ell^p$ spaces, or the symmetric Tsirelson space.

References

Bartle, R. G. (1977). "MR0402468 (53 #6288) (Review of Per Enflo's "A counterexample to the approximation problem in Banach spaces" Acta Mathematica 130 (1973), 309–317)". Mathematical Reviews. MR 402468.
Enflo, P.: A counterexample to the approximation property in Banach spaces. Acta Math. 130, 309–317(1973).
Grothendieck, A.: Produits tensoriels topologiques et espaces nucleaires. Memo. Amer. Math. Soc. 16 (1955).
Halmos, Paul R. (1978). "Schauder bases". American Mathematical Monthly 85 (4): 256–257. doi:10.2307/2321165. JSTOR 2321165. MR 488901.
Paul R. Halmos, "Has progress in mathematics slowed down?" Amer. Math. Monthly 97 (1990), no. 7, 561—588. MR 1066321
William B. Johnson "Complementably universal separable Banach spaces" in Robert G. Bartle (ed.), 1980 Studies in functional analysis, Mathematical Association of America.
Kwapień, S. "On Enflo's example of a Banach space without the approximation property". Séminaire Goulaouic–Schwartz 1972—1973: Équations aux dérivées partielles et analyse fonctionnelle, Exp. No. 8, 9 pp. Centre de Math., École Polytech., Paris, 1973. MR 407569
Lindenstrauss, J.; Tzafriri, L.: Classical Banach Spaces I, Sequence spaces, 1977.
Nedevski, P.; Trojanski, S. (1973). "P. Enflo solved in the negative Banach's problem on the existence of a basis for every separable Banach space". Fiz.-Mat. Spis. Bulgar. Akad. Nauk. 16 (49): 134–138. MR 458132.
Pietsch, Albrecht (2007). History of Banach spaces and linear operators. Boston, MA: Birkhäuser Boston, Inc. pp. xxiv+855 pp. ISBN 978-0-8176-4367-6. MR 2300779.
Karen Saxe, Beginning Functional Analysis, Undergraduate Texts in Mathematics, 2002 Springer-Verlag, New York.
Schaefer, Helmuth H.; Wolff, M.P. (1999). Topological Vector Spaces. GTM 3. New York: Springer-Verlag. ISBN 9780387987262.
Singer, Ivan. Bases in Banach spaces. II. Editura Academiei Republicii Socialiste România, Bucharest; Springer-Verlag, Berlin-New York, 1981. viii+880 pp. ISBN 3-540-10394-5. MR 610799

↑ Schaefer p. 108
↑ Schaefer p. 110
↑ Schaefer p. 109
↑ Schaefer p. 115

Functional analysis

Set / subset types	Absolutely convex Absorbing Balanced Bounded Convex Radial Star-shaped Symmetric Linear cone (subset) Convex cone (subset)

TVS types	Banach Barrelled Bornological Brauner F-space Finite-dimensional Fréchet (tame) Hilbert LF-space Locally convex Mackey Montel Nuclear Normed (norm) Quasinormed Reflexive Riesz Smith Stereotype Webbed Topological tensor product (of Hilbert spaces)

Mapping topologies	Dual Dual space Operator Strong (polar operator) Ultrastrong Weak (operator) Ultraweak Uniform convergence

Linear operators	Adjoint Bilinear (form) Bounded / Unbounded Closed Continuous / Discontinuous Compact Fredholm Hilbert–Schmidt Functionals (positive) Normal Nuclear Self-adjoint Strictly singular Trace class Transpose Unitary

Set operations	Algebraic interior (core) Interior Minkowski addition Polar

Banach algebras	C-algebras Spectrum (C-algebra radius) Spectral theory

Theorems	Banach–Alaoglu Banach–Saks Banach–Mazur Bessel's inequality Cauchy–Schwarz inequality Closed range Closed graph Eberlein–Šmulian Freudenthal spectral Gelfand–Mazur Goldstine Hahn–Banach (hyperplane separation) Kakutani fixed-point Lomonosov's invariant subspace Mackey–Arens Mazur's lemma M. Riesz extension Open mapping Parseval's identity Schauder fixed-point

Analysis	Bochner space Differentiation in Fréchet spaces Derivatives (Fréchet Gâteaux functional holomorphic) Integrals (Bochner Dunford Gelfand–Pettis regulated weak) Functional calculus (Borel continuous holomorphic) Inverse function theorem (Nash–Moser theorem) Vector measure