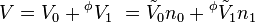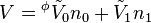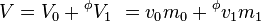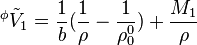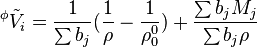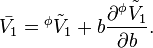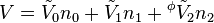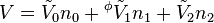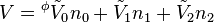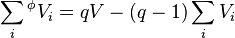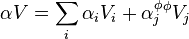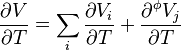Apparent molar property

An apparent molar property is a intensive quantity associated with a component of a solution that is back-computed from the corresponding property of the whole solution via a mole-weighted sum. For instance, the volume of a single-solute solution can be written as

V=V_0 + {}^\phi{V}_1 \ =\tilde{V}_{0} n_{0} + {}^\phi\tilde{V}_1 n_1 \,

where V₀ is the extensive volume of the pure solvent and 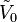$\tilde{V}_{0}$ its molar volume (at the same temperature and pressure as the solution), n₀ is the number of moles of solvent, 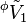${}^\phi\tilde{V}_1\,$ is the apparent molar volume of the solute, and n₁ is the number of moles of the solute in the solution.

This equation serves as the definition of 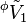${}^\phi\tilde{V}_1\,$ . The first term is equal to the volume of the same quantity of solvent with no solute, and the second term is the change of volume on addition of the solute. 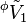${}^\phi\tilde{V}_1\,$ may then be considered as the molar volume of the solute if it is assumed that the molar volume of the solvent is unchanged by the addition of solute. However this assumption must often be considered unrealistic as shown in the Examples below, so that 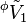${}^\phi\tilde{V}_1\,$ is described only as an apparent value.

Conversely, if we take the molar volume 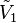$\tilde{V}_1$ of the solvent as the starting point, the apparent molar volume of the solvent can be defined via:

V= {}^\phi\tilde{V}_{0} n_{0} + \tilde{V}_1 n_1 \,

which emphasizes the change of the volume of the solvent in the mixing process.

Also the apparent quantities can be expressed using mass. This expression produces apparent specific quantities, like the apparent specific volume.

V=V_0 + {}^\phi{V}_1 \ =v_0 m_0 + {}^\phi{v}_1 m_1 \,

where the specific quantities are denoted with small letters.

Apparent (molar) properties are not constants (even at a given temperature), but are functions of the composition. At infinite dilution, an apparent molar property and the corresponding partial molar property become equal.

Some apparent molar properties that are commonly used are apparent molar enthalpy, apparent molar heat capacity, and apparent molar volume.

Relation to molality

The apparent (molar) volume of a solute can be expressed as a function of the molality b of that solute (and density of the solution and solvent):

{}^\phi\tilde{V}_1 = \frac{1}{b}( \frac{1}{\rho} - \frac{1}{\rho_0^0}) + \frac{M_1}{\rho}

For multicomponent systems the relation is slightly modified by the sum of molalities of solutes.

{}^\phi\tilde{V}_i = \frac{1}{\sum b_j}( \frac{1}{\rho} - \frac{1}{\rho_0^0}) + \frac{\sum b_j M_j}{\sum b_j \rho}

Relation to partial (molar) quantities

The relation between partial molar properties and the apparent ones can be derived from the definition of the apparent quantities and of the molality.

\bar{V_1}={}^\phi\tilde{V}_1 + b \frac{\partial {}^\phi\tilde{V}_1}{\partial b}.

The relation holds also for multicomponent mixtures, just that in this case subscript i is required.

Multicomponent mixtures/solutions

For multicomponent solutions, there is not an unambiguous definition of the apparent molar properties – with two solutes for example, there is still only one equation (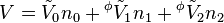 $V=\tilde{V}_{0} n_{0} + {}^\phi\tilde{V}_1 n_1+ {}^\phi\tilde{V}_2 n_2 \,$ ) to determine the two apparent volumes. (This is in contrast to partial molar properties, which are intrinsic properties of the materials and therefore unambiguously defined in multicomponent systems.)

If the apparent property of the solvent is also included, then q equations can be stated, one for each of the q components of the mixture, from which each apparent property can be calculated. In the case of ternary mixtures, one has

V=\tilde{V}_{0} n_{0} + \tilde{V}_1 n_1+ {}^\phi\tilde{V}_2 n_2 \,

V=\tilde{V}_{0} n_{0} + {}^\phi\tilde{V}_1 n_1+ \tilde{V}_2 n_2 \,

V={}^\phi\tilde{V}_{0} n_{0} + \tilde{V}_1 n_1+ \tilde{V}_2 n_2 \,

Sum

The sum of the apparent volumes of all components q is given by:

\sum_i {}^\phi{V}_i= q V - (q-1)\sum_i V_i \,

Derivative to state parameters

Applying the derivative to the apparent molar volume of a component in the mixture one gets the apparent molar expansivity.

\alpha V= \sum_i \alpha_i V_i + \alpha_j^{\phi} {}^\phi{V}_j

\frac{\partial V}{\partial T} = \sum_i \frac{\partial V_i}{\partial T} + \frac{\partial {}^\phi{V}_j}{\partial T}

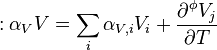
Equivalently: $:\alpha_V V = \sum_i \alpha_{V,i} V_i + \frac{\partial {}^\phi{V}_j}{\partial T}$

Examples

Electrolytes

The apparent molar volume of a salt is usually less than the molar volume of the solid salt. For instance, solid NaCl has a volume of 27 cm³ per mole, but the apparent molar volume at low concentrations is only 16.6 cc/mole. In fact, some aqueous electrolytes have negative apparent molar volumes: NaOH -6.7, LiOH -6.0, and Na₂CO₃ -6.7 cm³/mole.^[1] This means that their solutions in a given amount of water have a smaller volume than the same amount of pure water. (The effect is small however.) The physical reason is that nearby water molecules are strongly attracted to the ions so that they occupy less space.

Alcohol

Excess (Apparent) Volume of a Mixture of Ethanol and Water

Another example of apparent molar volume being less than the molar volume is the case of ethanol in water. For example, at 20 mass-percent ethanol, the solution has a volume of 1.0326 litres per kg at 20°C, while pure water is 1.0018 L/kg (1.0018 cc/g).^[2] This gives an apparent molar volume of (1.0326−0.8×1.0018)/0.2/0.04607 or 25.1 cc/mole (1.16 cc/g), whereas pure ethanol has a molar volume at this temperature of 27.5 cc/mole (1.27 cc/g). The nonideality of the solution is reflected by a slight decrease (roughly 2.2%) in the volume of the combined system upon mixing. As the percent ethanol goes up toward 100%, the apparent molar volume rises to the molar volume of pure ethanol.

Electrolyte - non-electrolyte systems

Apparent quantities can underline interactions in electrolyte - non-electrolyte systems which show interactions like salting in and salting out.

References

↑ Herbert Harned and Benton Owen, The Physical Chemistry of Electrolytic Solutions, 1950, p. 253.
↑ Calculated from data in the CRC Handbook of Chemistry and Physics, 49th edition.