Antimagic square
An antimagic square of order n is an arrangement of the numbers 1 to n2 in a square, such that the sums of the n rows, the n columns and the two diagonals form a sequence of 2n + 2 consecutive integers. The smallest antimagic squares have order 4.
Examples
|
|
Properties
In each of these two antimagic squares of order 4, the rows, columns and diagonals sum to ten different numbers in the range 29–38.
Antimagic squares form a subset of heterosquares which simply have each row, column and diagonal sum different. They contrast with magic squares where each sum is the same.
Open problems
- How many antimagic squares of a given order exist?
- Do antimagic squares exist for all orders greater than 3?
- Is there a simple proof that no antimagic square of order 3 exists?
Generalizations
A sparse antimagic square (SAM) is a square matrix of size n by n of nonnegative integers whose nonzero entries are the consecutive integers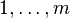 
for some 
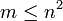, and whose row-sums and column-sums constitute a set of consecutive integers.[1] If the diagonals are included in the set of consecutive integers, the array is known as a sparse totally anti-magic square (STAM). Note that a STAM is not necessarily a SAM, and vice versa.
See also
References
- ↑ Gray, I. D.; MacDougall, J.A. (2006). "Sparse anti-magic squares and vertex-magic labelings of bipartite graphs". Discrete Mathematics 306: 2878–2892. doi:10.1016/j.disc.2006.04.032.