Anti-unification (computer science)
Anti-unification is the process of constructing a generalization common to two given symbolic expressions. As in unification, several frameworks are distinguished depending on which expressions (also called terms) are allowed, and which expressions are considered equal. If variables representing functions are allowed in an expression, the process is called higher-order anti-unification, otherwise first-order anti-unification. If the generalization is required to have an instance literally equal to each input expression, the process is called syntactical anti-unification, otherwise E-anti-unification, or anti-unification modulo theory.
An anti-unification algorithm should compute for given expressions a complete, and minimal generalization set, that is, a set covering all generalizations, and containing no redundant members, respectively. Depending on the framework, a complete and minimal generalization set may have one, finitely many, or possibly infinitely many members, or may not exist at all;[note 1] it cannot be empty, since a trivial generalization exists in any case. For first-order syntactical anti-unification, Gordon Plotkin[1][2] gave an algorithm that computes a complete and minimal singleton generalization set containing the so-called least general generalization (lgg).
Anti-unification should not be confused with dis-unification. The latter means the process of solving systems of inequations, that is of finding values for the variables such that all given inequations are satisfied.[note 2] This task is quite different from finding generalizations.
Prerequisites
Formally, an anti-unification approach presupposes
- An infinite set
 of variables. For higher-order anti-unification, it is convenient to choose
of variables. For higher-order anti-unification, it is convenient to choose  disjoint from the set of lambda-term bound variables.
disjoint from the set of lambda-term bound variables. - A set
 of terms such that
of terms such that 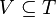 . For first-order and higher-order anti-unification,
. For first-order and higher-order anti-unification,  is usually the set of first-order terms (terms built from variable and function symbols) and lambda terms (terms containing some higher-order variables), respectively.
is usually the set of first-order terms (terms built from variable and function symbols) and lambda terms (terms containing some higher-order variables), respectively. - An equivalence relation
 on
on  , indicating which terms are considered equal. For higher-order anti-unification, usually
, indicating which terms are considered equal. For higher-order anti-unification, usually 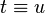 if
if  and
and  are alpha equivalent. For first-order E-anti-unification,
are alpha equivalent. For first-order E-anti-unification,  reflects the background knowledge about certain function symbols; for example, if
reflects the background knowledge about certain function symbols; for example, if 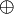 is considered commutative,
is considered commutative, 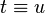 if
if  results from
results from  by swapping the arguments of
by swapping the arguments of 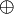 at some (possibly all) occurrences.[note 3] If there is no background knowledge at all, then only literally, or syntactically, identical terms are considered equal.
at some (possibly all) occurrences.[note 3] If there is no background knowledge at all, then only literally, or syntactically, identical terms are considered equal.
First-order term
Given a set  of variable symbols, a set
of variable symbols, a set  of constant symbols and sets
of constant symbols and sets 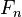 of
of  -ary function symbols, also called operator symbols, for each natural number
-ary function symbols, also called operator symbols, for each natural number 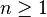 , the set of (unsorted first-order) terms
, the set of (unsorted first-order) terms  is recursively defined to be the smallest set with the following properties:[3]
is recursively defined to be the smallest set with the following properties:[3]
- every variable symbol is a term:
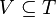 ,
, - every constant symbol is a term:
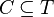 ,
, - from every
 terms
terms 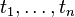 , and every
, and every  -ary function symbol
-ary function symbol 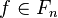 , a larger term
, a larger term 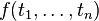 can be built.
can be built.
For example, if 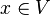 is a variable symbol,
is a variable symbol, 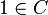 is a constant symbol, and
is a constant symbol, and 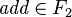 is a binary function symbol, then
is a binary function symbol, then 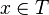 ,
, 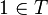 , and (hence)
, and (hence) 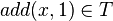 by the first, second, and third term building rule, respectively. The latter term is usually written as
by the first, second, and third term building rule, respectively. The latter term is usually written as 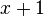 , using Infix notation and the more common operator symbol
, using Infix notation and the more common operator symbol 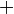 for convenience.
for convenience.
Higher-order term
Substitution
A substitution is a mapping 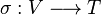 from variables to terms; the notation
from variables to terms; the notation 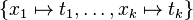 refers to a substitution mapping each variable
refers to a substitution mapping each variable 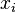 to the term
to the term 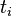 , for
, for 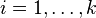 , and every other variable to itself. Applying that substitution to a term
, and every other variable to itself. Applying that substitution to a term  is written in postfix notation as
is written in postfix notation as 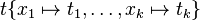 ; it means to (simultaneously) replace every occurrence of each variable
; it means to (simultaneously) replace every occurrence of each variable 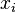 in the term
in the term  by
by 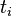 . The result
. The result 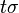 of applying a substitution
of applying a substitution  to a term
to a term  is called an instance of that term
is called an instance of that term  .
As a first-order example, applying the substitution
.
As a first-order example, applying the substitution 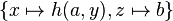 to the term
to the term
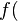 |
 |
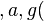 |
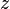 |
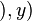 |
yields |
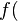 |
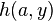 |
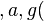 |
 |
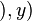 |
. |
Generalization, specialization
If a term  has an instance equivalent to a term
has an instance equivalent to a term  , that is, if
, that is, if 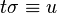 for some substitution
for some substitution  , then
, then  is called more general than
is called more general than  , and
, and  is called more special than, or subsumed by,
is called more special than, or subsumed by,  . For example,
. For example, 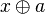 is more general than
is more general than 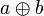 if
if 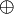 is commutative, since then
is commutative, since then 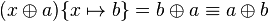 .
.
If  is literal (syntactic) identity of terms, a term may be both more general and more special than another one only if both terms differ just in their variable names, not in their syntactic structure; such terms are called variants, or renamings of each other.
For example,
is literal (syntactic) identity of terms, a term may be both more general and more special than another one only if both terms differ just in their variable names, not in their syntactic structure; such terms are called variants, or renamings of each other.
For example, 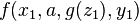 is a variant of
is a variant of 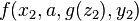 , since
, since 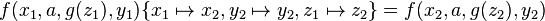 and
and 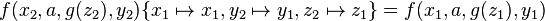 .
However,
.
However, 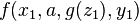 is not a variant of
is not a variant of 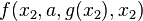 , since no substitution can transform the latter term into the former one, although
, since no substitution can transform the latter term into the former one, although 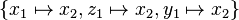 achieves the reverse direction.
The latter term is hence properly more special than the former one.
achieves the reverse direction.
The latter term is hence properly more special than the former one.
A substitution  is more special than, or subsumed by, a substitution
is more special than, or subsumed by, a substitution  if
if 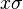 is more special than
is more special than 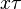 for each variable
for each variable  .
For example,
.
For example, 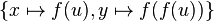 is more special than
is more special than 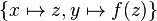 , since
, since 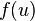 and
and 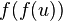 is more special than
is more special than 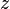 and
and 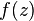 , respectively.
, respectively.
Anti-unification problem, generalization set
An anti-unification problem is a pair 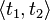 of terms.
A term
of terms.
A term  is a common generalization, or anti-unifier, of
is a common generalization, or anti-unifier, of 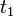 and
and 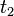 if
if 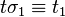 and
and 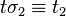 for some substitutions
for some substitutions 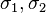 .
For a given anti-unification problem, a set
.
For a given anti-unification problem, a set  of anti-unifiers is called complete if each generalization subsumes some term
of anti-unifiers is called complete if each generalization subsumes some term 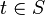 ; the set
; the set  is called minimal if none of its members subsumes another one.
is called minimal if none of its members subsumes another one.
First-order syntactical anti-unification
The framework of first-order syntactical anti-unification is based on  being the set of first-order terms (over some given set
being the set of first-order terms (over some given set  of variables,
of variables,  of constants and
of constants and 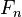 of
of  -ary function symbols) and on
-ary function symbols) and on  being syntactic equality.
In this framework, each anti-unification problem
being syntactic equality.
In this framework, each anti-unification problem 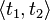 has a complete, and obviously minimal, singleton solution set
has a complete, and obviously minimal, singleton solution set 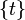 .
Its member
.
Its member  is called the least general generalization (lgg) of the problem, it has an instance syntactically equal to
is called the least general generalization (lgg) of the problem, it has an instance syntactically equal to 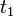 and another one syntactically equal to
and another one syntactically equal to 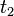 .
Any common generalization of
.
Any common generalization of 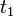 and
and 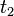 subsumes
subsumes  .
The lgg is unique up to variants: if
.
The lgg is unique up to variants: if 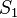 and
and 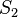 are both complete and minimal solution sets of the same syntactical anti-unification problem, then
are both complete and minimal solution sets of the same syntactical anti-unification problem, then 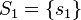 and
and 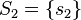 for some terms
for some terms 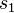 and
and 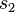 , that are renamings of each other.
, that are renamings of each other.
Plotkin[1][2] has given an algorithm to compute the lgg of two given terms.
It presupposes an injective mapping 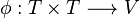 , that is, a mapping assigning each pair
, that is, a mapping assigning each pair 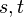 of terms an own variable
of terms an own variable 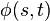 , such that no two pairs share the same variable.
[note 4]
The algorithm consists of two rules:
, such that no two pairs share the same variable.
[note 4]
The algorithm consists of two rules:
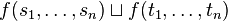
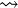
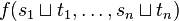

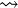
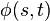
if previous rule not applicable
For example, 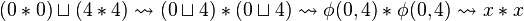 ; this least general generalization reflects the common property of both inputs of being square numbers.
; this least general generalization reflects the common property of both inputs of being square numbers.
Plotkin used his algorithm to compute the "relative least general generalization (rlgg)" of two clause sets in first-order logic, which was the basis of the Golem approach to inductive logic programming.
First-order anti-unification modulo theory
- Jacobson, Erik (Jun 1991), Unification and Anti-Unification, Technical Report
- Østvold, Bjarte M. (Apr 2004), A Functional Reconstruction of Anti-Unification, NR Note, DART/04/04, Norwegian Computing Center
- Boytcheva, Svetla; Markov, Zdravko (2002). "An Algorithm for Inducing Least Generalization Under Relative Implication".
- Kutsia, Temur; Levy, Jordi; Villaret, Mateu (2014). "Anti-Unification for Unranked Terms and Hedges". Journal of Automated Reasoning (Springer) 52 (2): 155–190. doi:10.1007/s10817-013-9285-6. Software.
Equational theories
- One associative and commutative operation: Pottier, Loic (Feb 1989), Algorithms des completion et generalisation en logic du premier ordre; Pottier, Loic (1989), Generalisation de termes en theorie equationelle – Cas associatif-commutatif, INRIA Report 1056, INRIA
- Commutative theories: Baader, Franz (1991). "Unification, Weak Unification, Upper Bound, Lower Bound, and Generalization Problems". Proc. 4th Conf. on Rewriting Techniques and Applications (RTA). LNCS 488. Springer. pp. 86–91.
- Free monoids: Biere, A. (1993), Normalisierung, Unifikation und Antiunifikation in Freien Monoiden, Univ. Karlsruhe, Germany
- Regular congruence classes: Heinz, Birgit (Dec 1995), Anti-Unifikation modulo Gleichungstheorie und deren Anwendung zur Lemmagenerierung, GMD Berichte 261, TU Berlin, ISBN 3-486-23873-6; Burghardt, Jochen (2005). "E-Generalization Using Grammars". Artificial Intelligence Journal (Elsevier) 165 (1): 1–35. doi:10.1016/j.artint.2005.01.008.
- A-, C-, AC-, ACU-theories with ordered sorts: Alpuente, Maria; Escobar, Santiago; Espert, Javier; Meseguer, Jose (2014). "A modular order-sorted equational generalization algorithm". Information and Computation (Elsevier) 235: 98–136. doi:10.1016/j.ic.2014.01.006.
First-order sorted anti-unification
- Taxonomic sorts: Frisch, Alan M.; Page, David (1990). "Generalisation with Taxonomic Information". AAAI: 755–761.; Frisch, Alan M.; Page Jr., C. David (1991). "Generalizing Atoms in Constraint Logic". Proc. Conf. on Knowledge Representation.; Frisch, A.M.; Page, C.D. (1995). "Building Theories into Instantiation". In Mellish, C.S. Proc. 14th IJCAI. Morgan Kaufmann. pp. 1210–1216.
- Feature terms: Plaza, E. (1995). "Cases as Terms: A Feature Term Approach to the Structured Representation of Cases". Proc. 1st International Conference on Case-Based Reasoning (ICCBR). LNCS 1010. Springer. pp. 265–276. ISSN 0302-9743.
- Idestam-Almquist, Peter (Jun 1993). "Generalization under Implication by Recursive Anti-Unification". Proc. 10th Conf. on Machine Learning. Morgan Kaufmann. pp. 151–158.
- Fischer, Cornelia (May 1994), PAntUDE – An Anti-Unification Algorithm for Expressing Refined Generalizations, Research Report, TM-94-04, DFKI
- A-, C-, AC-, ACU-theories with ordered sorts: see above
Applications
- Program analysis: Bulychev, Peter; Minea, Marius (2008). "Duplicate Code Detection Using Anti-Unification".; Bulychev, Peter E.; Kostylev, Egor V.; Zakharov, Vladimir A. (2009). "Anti-Unification Algorithms and their Applications in Program Analysis".
- Code factoring: Cottrell, Rylan (Sep 2008), Semi-automating Small-Scale Source Code Reuse via Structural Correspondence, Univ. Calgary
- Induction proving: Heinz, Birgit (1994), Lemma Discovery by Anti-Unification of Regular Sorts, Technical Report, 94-21, TU Berlin
- Information Extraction: Thomas, Bernd (1999). "Anti-Unification Based Learning of T-Wrappers for Information Extraction". AAAI Technical Report. WS-99-11: 15–20.
- Case-based reasoning: Armengol, Eva; Plaza, Enric (2005). "Using Symbolic Descriptions to Explain Similarity on CBR".
Anti-unification of trees and linguistic applications
- Parse trees for sentences can be subject to least general generalization to derive a maximal common sub-parse trees for language learning. There are applications in search and text classification.[4]
- Parse thickets for paragraphs as graphs can be subject to least general generalization.[5]
- Operation of generalization commutes with the operation of transition from syntactic (parse trees) to semantic (symbolic expressions) level. The latter can then be subject to conventional anti-unification.[6][7]
Higher-order anti-unification
- Calculus of constructions: Pfenning, Frank (Jul 1991). "Unification and Anti-Unification in the Calculus of Constructions". Proc. 6th LICS. Springer. pp. 74–85.
- Simply-typed lambda calculus (Input: Terms in the eta-long beta-normal form. Output: higher-order patterns): Baumgartner, Alexander; Kutsia, Temur; Levy, Jordi; Villaret, Mateu (Jun 2013). A Variant of Higher-Order Anti-Unification. Proc. RTA 2013. Vol. 21 of LIPIcs. Schloss Dagstuhl, 113-127. Software.
- Restricted Higher-Order: Wagner, Ulrich (Apr 2002), Combinatorically Restricted Higher Order Anti-Unification, TU Berlin; Schmidt, Martin (Sep 2010), Restricted Higher-Order Anti-Unification for Heuristic-Driven Theory Projection, PICS-Report, 31-2010, Univ. Osnabrück, Germany, ISSN 1610-5389
Notes
- ↑ Complete generalization sets always exist, but it may be the case that every complete generalization set is non-minimal.
- ↑ Comon referred in 1986 to inequation-solving as "anti-unification", which nowadays has become quite unusual. Comon, Hubert (1986). "Sufficient Completeness, Term Rewriting Systems and 'Anti-Unification'". Proc. 8th International Conference on Automated Deduction. LNCS 230. Springer. pp. 128–140.
- ↑ E.g.

- ↑ From a theoretical viewpoint, such a mapping exists, since both
 and
and 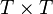 are countably infinite sets; for practical purposes,
are countably infinite sets; for practical purposes,  can be built up as needed, remembering assigned mappings
can be built up as needed, remembering assigned mappings 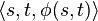 in a hash table.
in a hash table.
References
- ↑ 1.0 1.1 Plotkin, Gordon D. (1970). Meltzer, B.; Michie, D., eds. "A Note on Inductive Generalization". Machine Intelligence (Edinburgh University Press) 5: 153–163.
- ↑ 2.0 2.1 Plotkin, Gordon D. (1971). Meltzer, B.; Michie, D., eds. "A Further Note on Inductive Generalization". Machine Intelligence (Edinburgh University Press) 6: 101–124.
- ↑ C.C. Chang, H. Jerome Keisler (1977). A. Heyting and H.J. Keisler and A. Mostowski and A. Robinson and P. Suppes, ed. Model Theory. Studies in Logic and the Foundation of Mathematics 73. North Holland.; here: Sect.1.3
- ↑ Boris Galitsky, Josep Lluís de la Rose, Gabor Dobrocsi (2011). "Mapping Syntactic to Semantic Generalizations of Linguistic Parse Trees". FLAIRS Conference.
- ↑ Boris Galitsky, Kuznetsov SO, Usikov DA (2013). "Parse Thicket Representation for Multi-sentence Search". Lecture Notes in Computer Science 7735: 1072–1091. doi:10.1007/978-3-642-35786-2_12.
- ↑ Boris Galitsky, Gabor Dobrocsi, Josep Lluís de la Rosa, Sergei O. Kuznetsov (2010). "From Generalization of Syntactic Parse Trees to Conceptual Graphs". Lecture Notes in Computer Science 6208: 185–190. doi:10.1007/978-3-642-14197-3_19.
- ↑ Boris Galitsky, de la Rosa JL, Dobrocsi G. (2012). "Inferring the semantic properties of sentences by mining syntactic parse trees". Data & Knowledge Engineering. 81-82: 21–45. doi:10.1016/j.datak.2012.07.003.