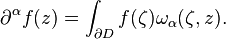Andreotti–Norguet formula
The Andreotti–Norguet formula, first introduced by Aldo Andreotti and François Norguet (1964, 1966),[1] is a higher–dimensional analogue of Cauchy integral formula for expressing the derivatives of a holomorphic function. Precisely, this formula express the value of the partial derivative of any multiindex order of a holomorphic function of several variables,[2] in any interior point of a given bounded domain, as a hypersurface integral of the values of the function on the boundary of the domain itself. In this respect, it is analogous and generalizes the Bochner–Martinelli formula,[3] reducing to it when the absolute value of the multiindex order of differentiation is 0.[4] When considered for functions of n = 1 complex variables, it reduces to the ordinary Cauchy formula for the derivative of a holomorphic function:[5] however, when n > 1, its integral kernel is not obtainable by simple differentiation of the Bochner–Martinelli kernel.[6]
Historical note
The Andreotti–Norguet formula was first published in the research announcement (Andreotti & Norguet 1964, p. 780):[7] however, its full proof was only published later in the paper (Andreotti & Norguet 1966, pp. 207–208).[8] Another, different proof of the formula was given by Martinelli (1975).[9] In 1977 and 1978, Lev Aizenberg gave still another proof and gave a generalization of the formula by using the Cauchy–Fantappiè–Leray kernel instead of the Bochner–Martinelli kernel.[10]
The Andreotti–Norguet integral representation formula
The notation adopted in the following description of the integral representation formula is the one used by Kytmanov (1995, p. 9) and by Kytmanov & Myslivets (2010, p. 20): the notations used in the original works and in other references, though equivalent, are significantly different.[11] Precisely, it is assumed that
- n > 1 is a fixed natural number,
- ζ, z ∈ ℂn are complex vectors,
- α = (α1,...,αn) ∈ ℕn is a multiindex whose absolute value is |α|,
- D ⊂ ℂn is a bounded domain whose closure is D,
- A(D) is the function space of functions holomorphic on the interior of D and continuous on its boundary ∂D.
- the iterated Wirtinger derivatives of order α of a given complex valued function f ∈ A(D) are expressed using the following simplified notation:
The Andreotti–Norguet kernel
Definition 1. For every multiindex α, the Andreotti–Norguet kernel ωα (ζ, z) is the following differential form in ζ of bidegree (n, n − 1):
where I = (1,...,1) ∈ ℕn and
The integral formula
Theorem 1 (Andreotti and Norguet). For every function f ∈ A(D), every point z ∈ D and every multiindex α, the following integral representation formula holds
See also
Notes
- ↑ For a brief historical sketch, see the "historical section" of the present entry.
- ↑ Partial derivatives of a holomorphic function of several complex variables are defined as partial derivatives respect to its complex arguments, i.e. as Wirtinger derivatives.
- ↑ See (Aizenberg & Yuzhakov 1983, p. 38), Kytmanov (1995, p. 9), Kytmanov & Myslivets (2010, p. 20) and (Martinelli 1984, pp. 152–153).
- ↑ As remarked in (Kytmanov 1995, p. 9) and (Kytmanov & Myslivets 2010, p. 20).
- ↑ As remarked by Aizenberg & Yuzhakov (1983, p. 38).
- ↑ See the remarks by Aizenberg & Yuzhakov (1983, p. 38) and Martinelli (1984, p. 153, footnote (1)).
- ↑ As correctly stated by Aizenberg & Yuzhakov (1983, p. 250, §5) and Kytmanov (1995, p. 9). Martinelli (1984, p. 153, footnote (1)) cites only the later work (Andreotti & Norguet 1966) which, however, contains the full proof of the formula.
- ↑ See (Martinelli 1984, p. 153, footnote (1)).
- ↑ According to Aizenberg & Yuzhakov (1983, p. 250, §5), Kytmanov (1995, p. 9), Kytmanov & Myslivets (2010, p. 20) and Martinelli (1984, p. 153, footnote (1)), who does not describe his results in this reference, but merely mentions them.
- ↑ See (Aizenberg 1993, p.289, §13), (Aizenberg & Yuzhakov 1983, p. 250, §5), the references cited in those sources and the brief remarks by Kytmanov (1995, p. 9), Kytmanov & Myslivets (2010, p. 20): each of these works report Aizenberg's proof.
- ↑ Compare, for example, the original ones by Andreotti and Norguet (1964, p. 780, 1966, pp. 207–208) and those used by Aizenberg & Yuzhakov (1983, p. 38), also briefly described in the .
References
- Aizenberg, Lev (1993) [1990], Carleman's Formulas in Complex Analysis. Theory and applications, Mathematics and Its Applications 244 (2nd ed.), Dordrecht–Boston–London: Kluwer Academic Publishers, pp. xx+299, doi:10.1007/978-94-011-1596-4, ISBN 0-7923-2121-9, MR 1256735, Zbl 0783.32002, revised translation of the 1990 Russian original.
- Aizenberg, L. A.; Yuzhakov, A. P. (1983) [1979], Integral Representations and Residues in Multidimensional Complex Analysis, Translations of Mathematical Monographs 58, Providence R.I.: American Mathematical Society, pp. x+283, ISBN 0-8218-4511-X, MR 0735793, Zbl 0537.32002.
- Andreotti, Aldo; Norguet, François (20 January 1964), "Problème de Levi pour les classes de cohomologie", Comptes rendus hebdomadaires des séances de l'Académie des Sciences (in French) 258 (Première partie): 778–781, MR 0159960, Zbl 0124.38803.
- Andreotti, Aldo; Norguet, François (1966), "Problème de Levi et convexité holomorphe pour les classes de cohomologie", Annali della Scuola Normale Superiore di Pisa, Classe di Scienze, Serie III, (in French) 20 (2): 197–241, MR 199439, Zbl 0154.3350.
- Berenstein, Carlos A.; Gay, Roger; Vidras, Alekos; Yger, Alain (1993), Residue currents and Bezout identities, Progress in Mathematics 114, Basel–Berlin–Boston: Birkhäuser Verlag, pp. xi+158, doi:10.1007/978-3-0348-8560-7, ISBN 3-7643-2945-9, MR 1249478, Zbl 0802.32001 ISBN 0-8176-2945-9, ISBN 978-3-0348-8560-7.
- Kytmanov, Alexander M. (1995) [1992], The Bochner–Martinelli integral and its applications, Birkhäuser Verlag, pp. xii+305, ISBN 978-3-7643-5240-0, MR 1409816, Zbl 0834.32001.
- Kytmanov, Alexander M.; Myslivets, Simona G. (2010), Интегральные представления и их приложения в многомерном комплексном анализе, Красноярск: СФУ, p. 389, ISBN 978-5-7638-1990-8 (English translation of title:"Integral representations and their application in multidimensional complex analysis").
- Martinelli, Enzo (1975), "Sopra una formula di Andreotti–Norguet", Bollettino dell'Unione Matematica Italiana, IV Serie (in Italian) 11 (3, Supplemento): 455–457, MR 0390270, Zbl 0317.32006. Collection of articles dedicated to Giovanni Sansone on the occasion of his eighty-fifth birthday.
- Martinelli, Enzo (1984), Introduzione elementare alla teoria delle funzioni di variabili complesse con particolare riguardo alle rappresentazioni integrali, Contributi del Centro Linceo Interdisciplinare di Scienze Matematiche e Loro Applicazioni (in Italian) 67, Rome: Accademia Nazionale dei Lincei, pp. 236+II. "Elementary introduction to the theory of functions of complex variables with particular regard to integral representations" (English translation of the title reads) is a textbook, published by the Accademia Nazionale dei Lincei, taken from the notes from a course held by Martinelli when he was in charge to the academy as a "Professore Linceo".
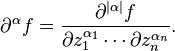
![\omega_\alpha(\zeta,z) = \frac{(n-1)!\alpha_1!\cdots\alpha_n!}{(2\pi i)^n}
\sum_{j=1}^n\frac{(-1)^{j-1}(\bar\zeta_j-\overline z_j) \, d\bar\zeta^{\alpha+I}[j] \and d\zeta}{\left(|z_1-\zeta_1|^{2(\alpha_1+1)} + \cdots + |z_n-\zeta_n|^{2(\alpha_n+1)}\right)^n},](../I/m/1814d2e02c20bf2fe12c0311808a8db0.png)
![d\bar\zeta^{\alpha+I}[j] = d\bar\zeta_1^{\alpha_1+1} \and \cdots \and d\bar\zeta_{j-1}^{\alpha_{j+1}+1} \and d\bar\zeta_{j+1}^{\alpha_{j-1}+1} \and \cdots \and d\bar\zeta_n^{\alpha_n+1}](../I/m/d433b0f39f043ee5f5421f447a953d6c.png)