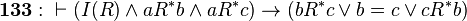Ancestral relation
In mathematical logic, the ancestral relation (often shortened to ancestral) of a binary relation R is defined as below.
Ancestral relations make their first appearance in Frege's Begriffsschrift. Frege later employed them in his Grundgesetze as part of his definition of the finite cardinals. Hence the ancestral was a key part of his search for a logicist foundation of arithmetic.
Definition
The numbered propositions below are taken from his Begriffsschrift and recast in contemporary notation.
A property P is called R-hereditary if, whenever x is P and xRy holds, then y is also P:
Frege defined b to be an R-ancestor of a, written aR*b, if b has every R-hereditary property that all objects x such that aRx have:
The ancestral is a transitive relation:
Let the notation I(R) denote that R is functional (Frege calls such relations "many-one"):
If R is functional, then the ancestral of R is what nowadays is called connected:
Relationship to transitive closure
The Ancestral relation 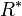 is equal to the transitive closure
is equal to the transitive closure 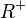 of
of  . Indeed,
. Indeed, 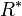 is transitive (see 98 above),
is transitive (see 98 above), 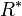 contains
contains  (indeed, if aRb then, of course, b has every R-hereditary property that all objects x such that aRx have, because b is one of them), and finally,
(indeed, if aRb then, of course, b has every R-hereditary property that all objects x such that aRx have, because b is one of them), and finally, 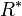 is contained in
is contained in 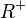 (indeed, assume
(indeed, assume 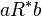 ; take the property
; take the property 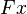 to be
to be 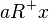 ; then the two premises,
; then the two premises, 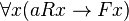 and
and 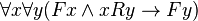 , are obviously satisfied; therefore,
, are obviously satisfied; therefore, 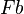 , which means
, which means 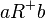 , by our choice of
, by our choice of 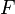 ). See also Boolos's book below, page 8.
). See also Boolos's book below, page 8.
Discussion
Principia Mathematica made repeated use of the ancestral, as does Quine's (1951) Mathematical Logic.
However, it is worth noting that the ancestral relation cannot be defined in first-order logic, and following the resolution of Russell's paradox both Frege and Quine largely considered the use of second-order logic a questionable approach. In particular, Quine did not consider second-order logic to be "logic" at all, despite his reliance upon it for his 1951 book (which largely retells Principia in abbreviated form, for which second-order logic is required to fit its theorems).
See also
References
- George Boolos, 1998. Logic, Logic, and Logic. Harvard Univ. Press.
- Ivor Grattan-Guinness, 2000. In Search of Mathematical Roots. Princeton Univ. Press.
- Willard Van Orman Quine, 1951 (1940). Mathematical Logic. Harvard Univ. Press. ISBN 0-674-55451-5.
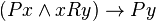
![\mathbf{76:}\ \vdash aR^*b \leftrightarrow \forall F [\forall x (aRx \to Fx) \land \forall x \forall y (Fx \land xRy \to Fy) \to Fb]](../I/m/b0b0125847e730fe9bef43251442c134.png)
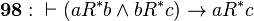
![\mathbf{115:}\ \vdash I(R) \leftrightarrow \forall x \forall y \forall z [(xRy \land xRz) \rightarrow y=z]](../I/m/fa0063c9bd068cd4f6de9fef1c5af8c8.png)