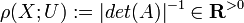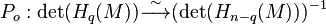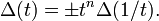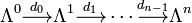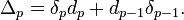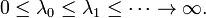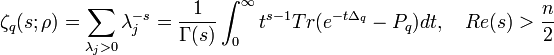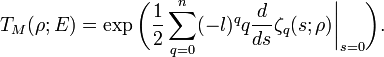Analytic torsion
In mathematics, Reidemeister torsion (or R-torsion, or Reidemeister–Franz torsion) is a topological invariant of manifolds introduced by Kurt Reidemeister (Reidemeister (1935)) for 3-manifolds and generalized to higher dimensions by Franz (1935) and de Rham (1936). Analytic torsion (or Ray–Singer torsion) is an invariant of Riemannian manifolds defined by Ray and Singer (1971, 1973a, 1973b) as an analytic analogue of Reidemeister torsion. Cheeger (1977, 1979) and Müller (1978) proved Ray and Singer's conjecture that Reidemeister torsion and analytic torsion are the same for compact Riemannian manifolds.
Reidemeister torsion was the first invariant in algebraic topology that could distinguish between spaces which are homotopy equivalent but not homeomorphic, and can thus be seen as the birth of geometric topology as a distinct field. It can be used to classify lens spaces.
Reidemeister torsion is closely related to Whitehead torsion; see (Milnor 1966). For later work on torsion see the books (Turaev 2002), (Nicolaescu 2002, 2003). And it had given one of important motivation to arithmetic topology. (Mazur)
Definition of analytic torsion
If M is a Riemannian manifold and E a vector bundle over M, then there is a Laplacian operator acting on the i-forms with values in E. If the eigenvalues on i-forms are λj then the zeta function ζi is defined to be
for s large, and this is extended to all complex s by analytic continuation. The zeta regularized determinant of the Laplacian acting on i-forms is
which is formally the product of the positive eigenvalues of the laplacian acting on i-forms. The analytic torsion T(M,E) is defined to be
Definition of Reidemeister torsion
Let  be a finite connected CW-complex with fundamental group
be a finite connected CW-complex with fundamental group 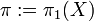 and universal cover
and universal cover 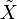 , and let
, and let  be an orthogonal finite-dimensional
be an orthogonal finite-dimensional 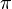 -representation. Suppose that
-representation. Suppose that
for all n. If we fix a cellular basis for 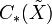 and an orthogonal
and an orthogonal 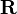 -basis for
-basis for  , then
, then ![D_* := U \otimes_{\mathbf{Z}[\pi]} C_*({\tilde X})](../I/m/68b6002353415ab5eb63413f2a9982b9.png) is a contractible finite based free
is a contractible finite based free 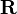 -chain complex. Let
-chain complex. Let 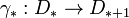 be any chain contraction of D*, i.e.
be any chain contraction of D*, i.e. 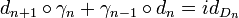 for all n. We obtain an isomorphism
for all n. We obtain an isomorphism 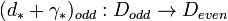 with
with 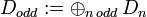 ,
, 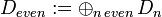 . We define the Reidemeister torsion
. We define the Reidemeister torsion
where A is the matrix of 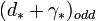 with respect to the given bases. The Reidemeister torsion
with respect to the given bases. The Reidemeister torsion 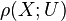 is independent of the choice of the cellular basis for
is independent of the choice of the cellular basis for 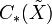 , the orthogonal basis for
, the orthogonal basis for  and the chain contraction
and the chain contraction 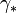 .
.
Let  be a compact smooth manifold, and let
be a compact smooth manifold, and let 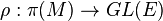 be a unimodular representation.
be a unimodular representation.  has a smooth triangulation. For any choice of a volume
has a smooth triangulation. For any choice of a volume 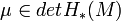 , we get an invariant
, we get an invariant 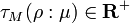 . Then we call the positive real number
. Then we call the positive real number 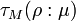 the Reidemiester torsion of the manifold
the Reidemiester torsion of the manifold  respect to
respect to  and
and  .
.
A short history of Reidemeister torsion
Reidemeister torsion was first used to combinatorially classify 3-dimensional lens spaces in (Reidemeister 1935) by Reidemeister, and in higher-dimensional spaces by Franz. The classification includes examples of homotopy equivalent 3-dimensional manifolds which are not homeomorphic – at the time (1935) the classification was only up to PL homeomorphism, but later (Brody 1960) showed that this was in fact a classification up to homeomorphism.
J. H. C. Whitehead defined the "torsion" of a homotopy equivalence between finite complexes. This is a direct generalization of the Reidemeister, Franz, and de Rham concept; but is a more delicate invariant. Whitehead torsion provides a key tool for the study of combinatorial or differentiable manifolds with nontrivial fundamental group and is closely related to the concept of "simple homotopy type." see (Milnor 1966)
In 1960 Milnor discovered the duality relation of torsion invariants of manifolds and show that the (twisted) Alexander polynomial of knots is the Reidemister torsion of its knot complement in S3. (Milnor 1962) For each q the Poincaré duality 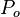 induces
induces
and then we obtain
The representation of the fundamental group of knot complement plays a central role in them. It gives the relation between knot theory and torsion invariants.
Cheeger–Müller theorem
Let 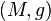 be an orientable compact Riemann manifold of dimension n and
be an orientable compact Riemann manifold of dimension n and 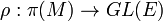 a representation of the fundamental group of
a representation of the fundamental group of  on a real vector space of dimension N. Then we can define the De Rham complex
on a real vector space of dimension N. Then we can define the De Rham complex
and the formal adjoint 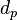 and
and 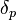 due to the flatness of
due to the flatness of 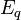 . And we also obtain the Laplacian on p-form as usual
. And we also obtain the Laplacian on p-form as usual
We assume 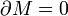 , then the Laplacian is a symmetric positive simipositive elliptic operator with pure point spectrum
, then the Laplacian is a symmetric positive simipositive elliptic operator with pure point spectrum
As same as the above definition we can define the zeta function associated with the Laplacian 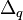 on
on 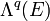 by
by
where  is the projection of
is the projection of 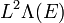 onto the kernel space
onto the kernel space 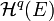 of the Laplacian
of the Laplacian 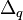 .
.
In 1967 Seeley proved that 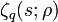 extends to a meromorphic function of
extends to a meromorphic function of 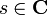 which is holomorphic at
which is holomorphic at 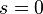 . (Seeley 1967)
. (Seeley 1967)
As in the case of an orthogonal representation, we define the analytic torsion 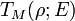 by
by
In 1971 D.B. Ray and I.M. Singer conjectured that 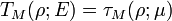 for any unitary representation
for any unitary representation  .Ray and Singer (1971) Independently, J. Cheeger Cheeger (1977, 1979) and W. Muller Müller (1978) proved the Ray–Singer conjecture. Their idea is considering the logarithm of torsions and their traces. Firstly for odd-dimensional manifolds they had proved the equality of two torsions and then for even-dimensional, which have some technical difficulties.
.Ray and Singer (1971) Independently, J. Cheeger Cheeger (1977, 1979) and W. Muller Müller (1978) proved the Ray–Singer conjecture. Their idea is considering the logarithm of torsions and their traces. Firstly for odd-dimensional manifolds they had proved the equality of two torsions and then for even-dimensional, which have some technical difficulties.
In later years, along with Atiyah–Patodi–Singer theorem, the Cheeger–Müller theorem, i.e. the equivalence of two torsions, forms the basis of Chern–Simons perturbation theory.
References
- Brody, E. J. (1960), "The topological classification of the lens spaces", Annals of Mathematics, 2 71 (1): 163–184, doi:10.2307/1969884, JSTOR 1969884
- Cheeger, Jeff (1977), "Analytic Torsion and Reidemeister Torsion", PNAS 74 (7): 2651–2654, doi:10.1073/pnas.74.7.2651, MR 0451312, PMC 431228, PMID 16592411
- Cheeger, Jeff (1979), "Analytic torsion and the heat equation", Ann. Of Math. (2) (Annals of Mathematics) 109 (2): 259–322, doi:10.2307/1971113, JSTOR 1971113, MR 0528965
- Franz, W. (1935), "Ueber die Torsion einer Ueberdeckung", J. Reine Angew. Math. 173: 245–254
- Milnor, J. (1962), "A Duality Theorem for Reidemeister Torsion.", Ann. of Math. 76 (1): 137–138, doi:10.2307/1970268
- Milnor, J. (1966), "Whitehead torsion.", Bull. Amer. Math. Soc. 72 (3): 358–426, doi:10.1090/S0002-9904-1966-11484-2, MR 0196736
- Mishchenko, A.S. (2001), "Reidemeister torsion", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Müller, Werner (1978), "Analytic torsion and R-torsion of Riemannian manifolds.", Adv. In Math. 28 (3): 233–305, doi:10.1016/0001-8708(78)90116-0, MR 0498252
- Nicolaescu, Liviu I. (2002), Notes on the Reidemeister torsion Online book
- Nicolaescu, Liviu I. (2003), The Reidemeister torsion of 3-manifolds, de Gruyter Studies in Mathematics 30, Berlin: Walter de Gruyter & Co., pp. xiv+249, ISBN 3-11-017383-2, MR 1968575
- Ray, D. B.; Singer, I. M. (1973a), "Analytic torsion for complex manifolds.", Ann. Of Math. (2) (Annals of Mathematics) 98 (1): 154–177, doi:10.2307/1970909, JSTOR 1970909, MR 0383463
- Ray, D. B.; Singer, I. M. (1973b), "Analytic torsion.", Partial differential equations, Proc. Sympos. Pure Math., XXIII, Providence, R.I.: Amer. Math. Soc., pp. 167–181, MR 0339293
- Ray, D. B.; Singer, I. M. (1971), "R-torsion and the Laplacian on Riemannian manifolds.", Advances in Math. 7 (2): 145–210, doi:10.1016/0001-8708(71)90045-4, MR 0295381
- Reidemeister, Kurt (1935), "Homotopieringe und Linsenräume", Abh. Math. Sem. Univ. Hamburg 11: 102–109, doi:10.1007/BF02940717
- de Rham, G. (1936), "Sur les nouveaux invariants de M. Reidemeister", Mat. Sb. , 1 (5): 737–743
- Turaev, Vladimir (2002), Torsions of 3-dimensional manifolds, Progress in Mathematics 208, Basel: Birkhäuser Verlag, pp. x+196, ISBN 3-7643-6911-6, MR 1958479
- Mazur, Barry, REMARKS ON THE ALEXANDER POLYNOMIAL
- Seeley, R. T. (1967), "Complex powers of an elliptic operator", in Calderón, Alberto P., Singular Integrals (Proc. Sympos. Pure Math., Chicago, Ill., 1966), Proceedings of Symposia in Pure Mathematics 10, Providence, R.I.: Amer. Math. Soc., pp. 288–307, ISBN 978-0-8218-1410-9, MR 0237943
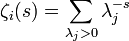
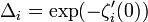
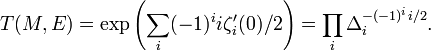
![H^\pi_n(X;U) := H_n(U \otimes_{\mathbf{Z}[\pi]} C_*({\tilde X})) = 0](../I/m/64824555f95a1fa579556fc95e5e55fc.png)