Analogical models
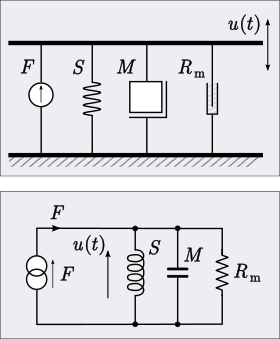
Analogical models are a method of representing a phenomenon of the world, often called the ‘target system’ by another, more understandable or analysable system. They are also called dynamical analogies.
Two open systems have analog representations (see illustration) if they are black box isomorphic systems.
Explanation
Analogizing is the process of representing information about a particular subject (the analogue or source system) by another particular subject (the target system). A simple type of analogy is one that is based on shared properties (Stanford Encyclopedia of Philosophy). Analogical models, also called "analog" or "analogue" models, therefore seek the analog systems that share properties with the target system as a means of representing the world. It is often practicable to construct source systems that are smaller and/or faster than the target system so that one can deduce a priori knowledge of target system behaviour. Analog devices are therefore those in which may differ in substance or structure but share properties of dynamic behaviour (Truit and Rogers, p. 1-3).
| “ | dynamical analogies establish the analogies between electrical, mechanical, acoustical, magnetic and electronic systems | ” |
(Olson 1958, p. 2).
For example, in analog electronic circuits, one can use voltage to represent an arithmetic quantity; operational amplifiers might then represent the arithmetic operations (addition, subtraction, multiplication, and division).Through the process of calibration these smaller/bigger, slower/faster systems are scaled up or down so that they match the functioning of the target system, and are therefore called analogs of the target system. Once the calibration has taken place, modellers speak of a one-to-one correspondence in behaviour between the primary system and its analog. Thus the behaviour of two systems can be determined by experimenting with one.
Creating an analogical model
Many different instruments and systems can be used to create an analogical model. A mechanical device can be used to represent mathematical calculations. For instance, the Phillips Hydraulic Computer used the flow of water to model economic systems (the target system); electronic circuits can be used to represent both physiological and ecological systems. When a model is run on either an analog or digital computer this is known as the process of simulation.
Mechanical analogies
There are any number of systems that could be used for mapping electrical phenomena to mechanical phenomena, but two principle systems are commonly used: the impedance analogy and the mobility analogy. The impedance analogy maps force to voltage whereas the mobility analogy maps force to current.
The impedance analogy preserves the analogy between electrical impedance and mechanical impedance but does not preserve the network topology. The mobility analogy preserves the network topology but does not preserve the analogy between impedances. Both preserve the correct energy and power relationships by making power conjugate pairs of variables analogous.
Hydraulic analogy
- In an hydraulic analogy, a water integrator might be used to perform the mathematical operation of integration.
Physiological analogies
- Francis Crick used the study of the visual system as a proxy for the study of awareness.
Formal analogies
- "The same equations have the same solutions." -- Richard Feynman
- For example, the inverse-square laws of gravitation and electromagnetism can be described by analogous equations on a geometrical basis, almost without regard to the physical details about masses and charges.
- In population ecology differential equations arise that are the same as those found in mechanics, albeit with different interpretations.[1]
- Recursion requires a similarity within a situation; for example, Archimedes used the myriad to count the number of grains of sand on a beach by using the concept of myriad myriads.
Dynamical analogies
Arising from his pioneering work in the field of acoustical engineering research, in 1958 (pp. 27–29) Dr. Harry F. Olson published a book of dynamical analogies that includes a table of equivalent elements in different systems such as electrical, acoustical, and mechanical systems. He claimed that the analogies presented would aid in solving various problems of dynamical systems and would help the analysis describing the performance of such systems.
Table of equivalents
| Through Variable | Across Variable | Energy Storage 1 | Energy Storage 2 | Energy Dissipation | |
|---|---|---|---|---|---|
| Electrical | Current (I) | Voltage (V) | Capacitor (C) | Inductor (L) | Resistor (R) |
| Mechanical Linear | Velocity (v) | Force (f) | Spring (K) | Mass (M) | Damper (B) |
| Mechanical Rotational | Angular Velocity (ω) | Torque (T) | Torsion Spring (κ) | Moment of Inertia (I) | Rotary Damper |
| Hydraulic | Volumetric flow rate (Q) | Pressure (p) | Accumulator | Pipe | Orifice |
Electronic circuit analogies
Hydraulic analog
A fluid or Hydraulic analogy of an electric circuit attempts to explain circuitry in terms of plumbing, where water represents the mobile sea of charge within metals, where pressure difference is analogy for Voltage, and where water's flow rate is an analogy for Electric current.
Analogue computers
Electronic circuits were used to model and simulate engineering systems such as aeroplanes and nuclear power plants before digital computers became widely available with fast enough turn over times to be practically useful. Electronic circuit instruments called analog computers were used to speed up circuit construction time. However analog computers like the norden bombsight could also consist of gears and pulleys in calculation.
Examples are Vogel and Ewel who published 'An Electrical Analog of a Trophic Pyramid' (1972, Chpt 11, pp. 105–121), Elmore and Sands (1949) who published circuits devised for research in nuclear physics and the study of fast electrical transients done under the Manhattan Project (however no circuits having application to weapon technology were included for security reasons), and Howard T. Odum (1994) who published circuits devised to analogically model ecological-economic systems at many scales of the geobiosphere.
Philosophical conundrum
The process of analogical modelling has philosophical difficulties. As noted in the Stanford Encyclopedia of Philosophy, there is the question of how the physical/biological laws of the target system relate to the analogical models created by humans to represent the target system. We seem to assume that the process of constructing analogical models gives us access to the fundamental laws governing the target system. However strictly speaking we only have empirical knowledge of the laws that hold true for the analogical system, and if the time constant for the target system is larger than the life cycle of human being (as in the case of the geobiosphere) it is therefore very difficult for any single human to empirically verify the validity of the extension of the laws of their model to the target system in their lifetime.
See also
|
References
- ↑ Ginzburg and Colyvan 2004; Colyvan and Ginzburg 2010
- Oliver Heaviside (1893), "A gravitational and electromagnetic analogy". The Electrician.
- Elmore and Sanders (1949) Electronics: Experimental Techniques, National Nuclear Energy Series, Manhattan Project Technical Section, Division V, Vol. 1, McGraw-Hill.
- Howard T. Odum (1994) Ecological and General Systems: and introduction to systems ecology, Colorado University Press.
- H.F. Olson (1958) Dynamical Analogies, 2nd ed., Van Nostrand, pp. 27–29.
- Truit and Rogers (1960) Basics of analog computers, John F. Rider Publishing, Inc., New York.
- Vogel and Ewel (1972) A Model Menagerie: Laboraratory Studies about Living Systems, Addison-Wesley.
- Mark Colyvan and Lev R. Ginzburg (2010) "Analogical Thinking in Ecology: Looking Beyond Disciplinary Boundaries", The Quarterly Review of Biology, 85(2): 171–82.
- Lev Ginzburg and Mark Colyvan (2004) Ecological Orbits: How Planets Move and Populations Grow, Oxford University Press, New York.