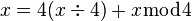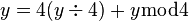Almost linear hash function

An almost linear function is a function h such that, for every inputs x and y, one of the following two equations hold:

  1. h(x+y)=h(x)+h(y)
  2. h(x+y)=h(x)+h(y)+1.

If equation 1 always holds, then h is a linear function. But if in some cases equation 2 holds, then h is almost linear.

The almost-linearity concept is mainly used with hash functions. A hash function can be used to map a large domain (e.g. the numbers between 0 and M − 1) to a much smaller domain (e.g. the numbers between 0 and m − 1, where m < M). It is easy to create a linear hash function, e.g. for every constant a, the following function is linear:

h(x)=a x \bmod m

However, this family of functions is missing some other features that are required from a hash function, e.g. it is not universal. In contrast, the following function is both universal and almost linear, for every odd constant a and for every M, m which are powers of 2:[1][2]

h(x)=(a x \mod M) \div (M/m)

where \div means integer division (taking only the integral part of the result and discarding the remainder).

For example, if M = 64, m = 16 and a = 1:

h(x)=(x \bmod 64) \div 4

For every x, y:

x = 4 (x\div 4) + x \bmod 4
y = 4 (y\div 4) + y \bmod 4
x+y = 4 (x\div 4 + y\div 4) + (x \bmod 4) + (y \bmod 4)

Hence, if (x \bmod 4) + (y \bmod 4) < 4, then it is discarded in the integer division by 4, and we get:

h(x+y) = x\div 4 + y\div 4 = h(x)+h(y)

The only other option is that 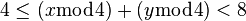4 \leq (x \bmod 4) + (y \bmod 4) < 8. In this case, dividing it by 4 gives an integer part of 1, and we get:

h(x+y) = x\div 4 + y\div 4 + 1 = h(x)+h(y)+1

This proves that h is an almost-linear function.

References

  1. ↑ Dietzfelbinger, M.; Hagerup, T.; Katajainen, J.; Penttonen, M. (1997). "A Reliable Randomized Algorithm for the Closest-Pair Problem". Journal of Algorithms 25: 19. doi:10.1006/jagm.1997.0873.
  2. ↑ Kopelowitz, Tsvi; Pettie, Seth; Porat, Ely (2014). "3SUM Hardness in (Dynamic) Data Structures". arXiv:1407.6756 [cs.DS].