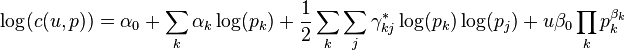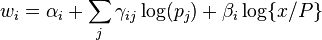Almost ideal demand system

The Almost Ideal Demand System (AIDS) (1980) is a consumer demand model used primarily by economists to study consumer behavior. The AIDS model gives an arbitrary first-order approximation to any demand system and has many desirable qualities of demand systems. For instance it satisfies the axioms of order, aggregates over consumers without invoking parallel linear Engel curves, is consistent with budget constraints, and is simple to estimate.

Model

The AIDS model is based on a first specification of a cost/expenditure function c(u,p):

\log(c(u,p))=\alpha_{0}+\sum_{k}\alpha_{k}\log(p_{k})+\frac{1}{2}\sum_{k}\sum_{j}\gamma_{kj}^{*}\log(p_{k})\log(p_{j})+u\beta_{0}\prod_{k}p_{k}^{\beta_{k}}

where p stands for the prices of the L goods, and u the utility level. This specification satisfies homogeneity of order 1 in prices, and is a second order approximation of any cost function.

From this, demand equations are derived (using Shephard's lemma), but are however simpler to put in term of budget shares:

w_{i}=\alpha_{i}+\sum_{j}\gamma_{ij}\log(p_{j})+\beta_{i}\log\{x/P\}

with x total expenditures, 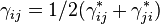$\gamma_{ij}=1/2(\gamma^*_{ij}+\gamma^*_{ji})$ , and P is a price index:

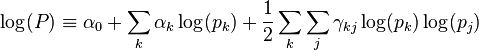\log(P)\equiv\alpha_{0}+\sum_{k}\alpha_{k}\log(p_{k})+\frac{1}{2}\sum_{k}\sum_{j}\gamma_{kj}\log(p_{k})\log(p_{j})

Under relevant constraints on the parameters 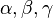$\alpha, \beta, \gamma$ , These budget shares equations share the properties of a demand function:

homogoeneous of degree 0 in prices and total expenditure
sum of budget shares add up to 1 (i.e., $\sum w_i=1$ )
satisfy the symmetry of the Slutsky matrix

Origin

The AIDS system is derived from the piglog model, which allows researchers to treat aggregate consumer behavior as if it were the outcome of a single maximizing consumer.

References

An Almost Ideal Demand System, Angus Deaton, John Muellbauer, The American Economic Review, Vol. 70, No. 3. (Jun., 1980), pp. 312-326.