Algebraic operation
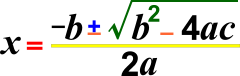
In mathematics, an algebraic operation is any one of the operations addition, subtraction, multiplication, division, raising to an integer power, and taking roots (fractional power). Algebraic operations are performed on an algebraic variable, term or expression,[1] and work in the same way as arithmetic operations.[2]
Notation
Multiplication symbols are usually omitted, and implied when there is no operator between two variables or terms, or when a coefficient is used. For example, 3 × x2 is written as 3x2, and 2 × x × y is written as 2xy.[3] Sometimes multiplication symbols are replaced with either a dot, or center-dot, so that x × y is written as either x . y or x · y. Plain text, programming languages, and calculators also use a single asterisk to represent the multiplication symbol,[4] and it must be explicitly used, for example, 3x is written as 3 * x.
Rather than using the obelus symbol, ÷, division is usual represented with a vinculum, a horizontal line, e.g. 3/x + 1. In plain text and programming languages a slash (also called a solidus) is used, e.g. 3 / (x + 1).
Exponents are usually formatted using superscripts, e.g. x2. In plain text, and in the TeX mark-up language, the caret symbol, ^, represents exponents, so x2 is written as x ^ 2.[5][6] In programming languages such as Ada,[7] Fortran,[8] Perl,[9] Python[10] and Ruby,[11] a double asterisk is used, so x2 is written as x ** 2.
The plus-minus sign, ±, is used as a shorthand notation for two expressions written as one, representing one expression with a plus sign, the other with a minus sign. For example y = x ± 1 represents the two equations y = x + 1 and y = x − 1. Sometimes it is used for denoting positive-or-negative term such as ±x.
Arithmetic vs algebraic operations
Algebraic operations work in the same way as arithmetic operations, as can be seen in the table below.
| Operation | Arithmetic Example |
Algebra Example |
Comments ≡ – means "equivalent to" ≢ – means "not equivalent to" |
|---|---|---|---|
| Addition | 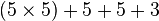
equivalent to:
|
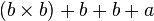
equivalent to:
|
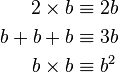 |
| Subtraction | 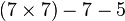
equivalent to:
|
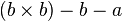
equivalent to:
|
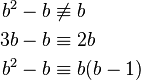 |
| Multiplication | 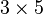 or or
or |
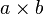 or or
or |
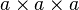 is the same as is the same as 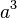 |
| Division | 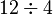 or or
|
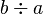 or or
|
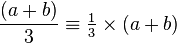 |
| Exponentiation | 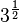 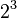 |
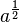 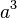 | 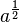 is the same as is the same as 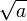 |
Note: the use of the letters  and
and  is arbitrary, and the examples would be equally valid if we had used
is arbitrary, and the examples would be equally valid if we had used  and
and  .
.
Properties of arithmetic and algebraic operations
| Property | Arithmetic Example |
Algebra Example |
Comments ≡ – means "equivalent to" ≢ – means "not equivalent to" |
|---|---|---|---|
| Commutativity | 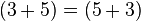 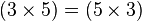 |
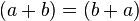 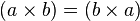 |
Addition and multiplication are commutative and associative[12] Subtraction and division are not e.g. |
| Associativity | 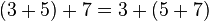 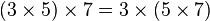 |
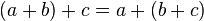 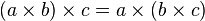 |
References
- ↑ William Smyth, Elementary algebra: for schools and academies, Publisher Bailey and Noyes, 1864, "Algebraic Operations"
- ↑ Horatio Nelson Robinson, New elementary algebra: containing the rudiments of science for schools and academies, Ivison, Phinney, Blakeman, & Co., 1866, page 7
- ↑ Sin Kwai Meng, Chip Wai Lung, Ng Song Beng, "Algebraic notation", in Mathematics Matters Secondary 1 Express Textbook, Publisher Panpac Education Pte Ltd, ISBN 9812738827, 9789812738820, page 68
- ↑ William P. Berlinghoff, Fernando Q. Gouvêa, Math through the Ages: A Gentle History for Teachers and Others, Publisher MAA, 2004, ISBN 0883857367, 9780883857366, page 75
- ↑ Ramesh Bangia, Dictionary of Information Technology, Publisher Laxmi Publications, Ltd., 2010, ISBN 9380298153, 9789380298153, page 212
- ↑ George Grätzer, First Steps in LaTeX, Publisher Springer, 1999, ISBN 0817641327, 9780817641320, page 17
- ↑ S. Tucker Taft, Robert A. Duff, Randall L. Brukardt, Erhard Ploedereder, Pascal Leroy, Ada 2005 Reference Manual, Volume 4348 of Lecture Notes in Computer Science, Publisher Springer, 2007, ISBN 3540693351, 9783540693352, page 13
- ↑ C. Xavier, Fortran 77 And Numerical Methods, Publisher New Age International, 1994, ISBN 812240670X, 9788122406702, page 20
- ↑ Randal Schwartz, brian foy, Tom Phoenix, Learning Perl, Publisher O'Reilly Media, Inc., 2011, ISBN 1449313140, 9781449313142, page 24
- ↑ Matthew A. Telles, Python Power!: The Comprehensive Guide, Publisher Course Technology PTR, 2008, ISBN 1598631586, 9781598631586, page 46
- ↑ Kevin C. Baird, Ruby by Example: Concepts and Code, Publisher No Starch Press, 2007, ISBN 1593271484, 9781593271480, page 72
- ↑ Ron Larson, Robert Hostetler, Bruce H. Edwards, Algebra And Trigonometry: A Graphing Approach, Publisher: Cengage Learning, 2007, ISBN 061885195X, 9780618851959, 1114 pages, page 7
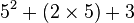
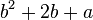
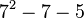
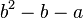
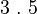
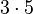
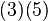
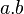
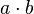
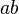
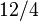 or
or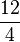
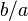 or
or
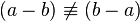
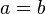 )
)