Algebraic closure

In mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics.

Using Zorn's lemma, it can be shown that every field has an algebraic closure,^[1]^[2]^[3] and that the algebraic closure of a field K is unique up to an isomorphism that fixes every member of K. Because of this essential uniqueness, we often speak of the algebraic closure of K, rather than an algebraic closure of K.

The algebraic closure of a field K can be thought of as the largest algebraic extension of K. To see this, note that if L is any algebraic extension of K, then the algebraic closure of L is also an algebraic closure of K, and so L is contained within the algebraic closure of K. The algebraic closure of K is also the smallest algebraically closed field containing K, because if M is any algebraically closed field containing K, then the elements of M that are algebraic over K form an algebraic closure of K.

The algebraic closure of a field K has the same cardinality as K if K is infinite, and is countably infinite if K is finite.^[3]

Examples

The fundamental theorem of algebra states that the algebraic closure of the field of real numbers is the field of complex numbers.

The algebraic closure of the field of rational numbers is the field of algebraic numbers.

There are many countable algebraically closed fields within the complex numbers, and strictly containing the field of algebraic numbers; these are the algebraic closures of transcendental extensions of the rational numbers, e.g. the algebraic closure of Q(π).

For a finite field of prime power order q, the algebraic closure is a countably infinite field that contains a copy of the field of order qⁿ for each positive integer n (and is in fact the union of these copies).^[4]

Existence of an algebraic closure and splitting fields

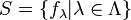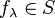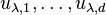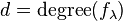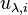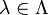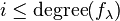Let $S = \{ f_{\lambda} | \lambda \in \Lambda\}$ be the set of all monic irreducible polynomials in K[x]. For each $f_{\lambda} \in S$ , introduce new variables $u_{\lambda,1},\ldots,u_{\lambda,d}$ where $d = {\rm degree}(f_{\lambda})$ . Let R be the polynomial ring over K generated by $u_{\lambda,i}$ for all $\lambda \in \Lambda$ and all $i \leq {\rm degree}(f_{\lambda})$ . Write

f_{\lambda} - \prod_{i=1}^d (x-u_{\lambda,i}) = \sum_{j=0}^{d-1} r_{\lambda,j} \cdot x^j \in R[x]

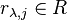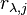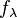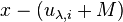with $r_{\lambda,j} \in R$ . Let I be the ideal in R generated by the $r_{\lambda,j}$ . By Zorn's lemma, there exists a maximal ideal M in R that contains I. Now R/M is an algebraic closure of K; every $f_{\lambda}$ splits as the product of the $x-(u_{\lambda,i} + M)$ .

The same proof also shows that for any subset S of K[x], there exists a splitting field of S over K.

Separable closure

An algebraic closure K^alg of K contains a unique separable extension K^sep of K containing all (algebraic) separable extensions of K within K^alg. This subextension is called a separable closure of K. Since a separable extension of a separable extension is again separable, there are no finite separable extensions of K^sep, of degree > 1. Saying this another way, K is contained in a separably-closed algebraic extension field. It is essentially unique (up to isomorphism).^[5]

The separable closure is the full algebraic closure if and only if K is a perfect field. For example, if K is a field of characteristic p and if X is transcendental over K, $K(X)(\sqrt[p]{X}) \supset K(X)$ is a non-separable algebraic field extension.

In general, the absolute Galois group of K is the Galois group of K^sep over K.^[6]

References

↑ McCarthy (1991) p.21
↑ M. F. Atiyah and I. G. Macdonald (1969). Introduction to commutative algebra. Addison-Wesley publishing Company. pp. 11-12.
↑ 3.0 3.1 Kaplansky (1972) pp.74-76
↑ Brawley, Joel V.; Schnibben, George E. (1989), "2.2 The Algebraic Closure of a Finite Field", Infinite Algebraic Extensions of Finite Fields, Contemporary Mathematics 95, American Mathematical Society, pp. 22–23, ISBN 978-0-8218-5428-0, Zbl 0674.12009 .
↑ McCarthy (1991) p.22
↑ Fried, Michael D.; Jarden, Moshe (2008). Field arithmetic. Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge 11 (3rd ed.). Springer-Verlag. p. 12. ISBN 978-3-540-77269-9. Zbl 1145.12001.

Kaplansky, Irving (1972). Fields and rings. Chicago lectures in mathematics (Second ed.). University of Chicago Press. ISBN 0-226-42451-0. Zbl 1001.16500.
McCarthy, Paul J. (1991). Algebraic extensions of fields (Corrected reprint of the 2nd ed.). New York: Dover Publications. Zbl 0768.12001.

Algebraic closure

Examples

Existence of an algebraic closure and splitting fields

Separable closure

See also

References