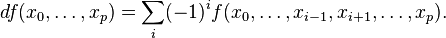Alexander–Spanier cohomology

In mathematics, particularly in algebraic topology, Alexander–Spanier cohomology is a cohomology theory for topological spaces.

History

It was introduced by J. W. Alexander (1935) for the special case of compact metric spaces, and by E. H. Spanier (1948) for all topological spaces, based on a suggestion of A. D. Wallace.

Definition

If X is a topological space and G is an abelian group, then there is a complex C whose pth term C^p is the set of all functions from X^p+1 to G with differential d given by

df(x_0,\ldots,x_p)= \sum_i(-1)^if(x_0,\ldots,x_{i-1},x_{i+1},\ldots,x_p).

It has a subcomplex C₀ of functions that vanish in a neighborhood of the diagonal. The Alexander–Spanier cohomology groups H^p(X,G) are defined to be the cohomology groups of the complex C/C₀.

Variants

It is also possible to define Alexander–Spanier homology (Massey 1978) and Alexander–Spanier cohomology with compact supports (Bredon 1997).

Connection to other cohomologies

The Alexander–Spanier cohomology groups coincide with Čech cohomology groups for compact Hausdorff spaces, and coincide with singular cohomology groups for locally finite complexes.

References

Alexander, J. W. (1935), "On the Chains of a Complex and Their Duals", Proceedings of the National Academy of Sciences of the United States of America (National Academy of Sciences) 21 (8): 509–511, doi:10.1073/pnas.21.8.509, ISSN 0027-8424, JSTOR 86360
Bredon, Glen E. (1997), Sheaf theory, Graduate Texts in Mathematics 170 (2nd ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-94905-5, MR 1481706
Massey, William S. (1978), "How to give an exposition of the Čech-Alexander-Spanier type homology theory", The American Mathematical Monthly 85 (2): 75–83, ISSN 0002-9890, JSTOR 2321782, MR 0488017
Massey, William S. (1978), Homology and cohomology theory. An approach based on Alexander-Spanier cochains., Monographs and Textbooks in Pure and Applied Mathematics 46, New York: Marcel Dekker Inc., ISBN 978-0-8247-6662-7, MR 0488016
Spanier, Edwin H. (1948), "Cohomology theory for general spaces", Annals of Mathematics. Second Series 49: 407–427, ISSN 0003-486X, JSTOR 1969289, MR 0024621