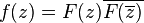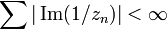Akhiezer's theorem

In the mathematical field of complex analysis, Akhiezer's theorem is a result about entire functions proved by Naum Akhiezer.^[1]

Statement

Let $f (z)$ be an entire function of exponential type $τ$ , with $f (x) \geq 0$ for real $x$ . Then the following are equivalent:

There exists an entire function $F$ , of exponential type $τ /2$ , having all its zeros in the (closed) upper half plane, such that

f(z)=F(z)\overline{F(\overline{z})}

One has:

\sum|\operatorname{Im}(1/z_{n})|<\infty

where $z n$ are the zeros of $f$ .

Remarks

It is not hard to show that the Fejér–Riesz theorem is a special case.^[2]

Notes

↑ see Akhiezer (1948).
↑ see Boas (1954) and Boas (1944) for references.

References

Boas, Jr., Ralph Philip (1954), Entire functions, New York: Academic Press Inc., pp. 124–132
Boas, Jr., R. P. (1944), "Functions of exponential type. I", Duke Math. J. 11: 9–15, doi:10.1215/s0012-7094-44-01102-6, ISSN 0012-7094
Akhiezer, N. I. (1948), "On the theory of entire functions of finite degree", Doklady Akad. Nauk SSSR (N.S.) 63: 475–478, MR 0027333