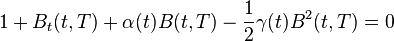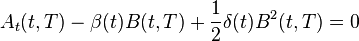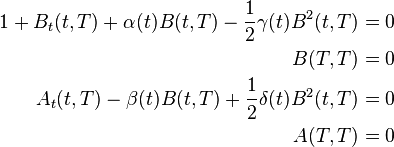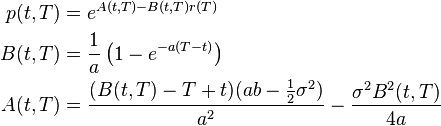Affine term structure model
An affine term structure model is a financial model that relates zero-coupon bond prices (i.e. the discount curve) to a spot rate model. It is particularly useful for inverting the yield curve – the process of determining spot rate model inputs from observable bond market data.
Background
Start with a stochastic short rate model 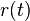 with dynamics
with dynamics
and a risk-free zero-coupon bond maturing at time 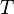 with price
with price 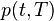 at time
at time 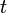 . If
. If
and 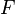 has the form
has the form
where  and
and 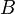 are deterministic functions, then the short rate model is said to have an affine term structure.
are deterministic functions, then the short rate model is said to have an affine term structure.
Existence
Using Ito's formula we can determine the constraints on 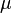 and
and 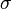 which will result in an affine term structure. Assuming the bond has an affine term structure and
which will result in an affine term structure. Assuming the bond has an affine term structure and 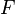 satisfies the term structure equation, we get
satisfies the term structure equation, we get
The boundary value
implies
Next, assume that 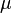 and
and 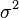 are affine in
are affine in  :
:
The differential equation then becomes
Because this formula must hold for all  ,
, 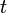 ,
, 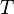 , the coefficient of
, the coefficient of  must equal zero.
must equal zero.
Then the other term must vanish as well.
Then, assuming 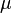 and
and 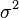 are affine in
are affine in  , the model has an affine term structure where
, the model has an affine term structure where  and
and 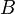 satisfy the system of equations:
satisfy the system of equations:
Models with ATS
Vasicek
The Vasicek model  has an affine term structure where
has an affine term structure where
References
- Bjork, Tomas (2009). Arbitrage Theory in Continuous Time, third edition. New York, NY: Oxford University Press. ISBN 978-0-19-957474-2.
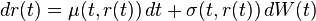
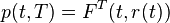
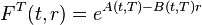
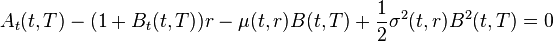
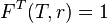
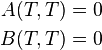
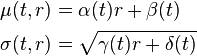
![A_t(t,T)-\beta(t)B(t,T)+\frac{1}{2}\delta(t)B^2(t,T)-\left[1+B_t(t,T)+\alpha(t)B(t,T)-\frac{1}{2}\gamma(t)B^2(t,T)\right]r=0](../I/m/ae495daf50ad4fa70030168ed2d79ae6.png)