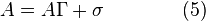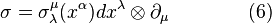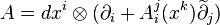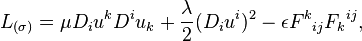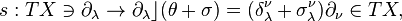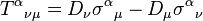Affine gauge theory
Affine gauge theory is classical gauge theory where gauge fields are affine connections on the tangent bundle over a smooth manifold  . For instance, these are gauge theory of dislocations in continuous media when
. For instance, these are gauge theory of dislocations in continuous media when 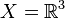 , the generalization of metric-affine gravitation theory when
, the generalization of metric-affine gravitation theory when  is a world manifold and, in particular, gauge theory of the fifth force.
is a world manifold and, in particular, gauge theory of the fifth force.
Affine tangent bundle
Being a vector bundle, the tangent bundle 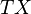 of an
of an  -dimensional manifold
-dimensional manifold  admits a natural structure of an affine bundle
admits a natural structure of an affine bundle 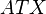 , called the affine tangent bundle, possessing bundle atlases with affine transition functions. It is associated to a principal bundle
, called the affine tangent bundle, possessing bundle atlases with affine transition functions. It is associated to a principal bundle 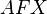 of affine frames in tangent space over
of affine frames in tangent space over  , whose structure group is a general affine group
, whose structure group is a general affine group 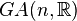 .
.
The tangent bundle 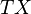 is associated to a principal linear frame bundle
is associated to a principal linear frame bundle 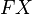 , whose structure group is a general linear group
, whose structure group is a general linear group 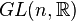 . This is a subgroup of
. This is a subgroup of 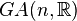 so that the latter is a semidirect product of
so that the latter is a semidirect product of 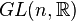 and a group
and a group 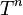 of translations.
of translations.
There is the canonical imbedding of 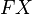 to
to 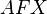 onto a reduced principal subbundle which corresponds to the canonical structure of a vector bundle
onto a reduced principal subbundle which corresponds to the canonical structure of a vector bundle 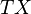 as the affine one.
as the affine one.
Given linear bundle coordinates
on the tangent bundle 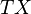 , the affine tangent bundle can be provided with affine bundle coordinates
, the affine tangent bundle can be provided with affine bundle coordinates
and, in particular, with the linear coordinates (1).
Affine gauge fields
The affine tangent bundle 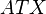 admits an affine connection
admits an affine connection  which is associated to a principal connection on an affine frame bundle
which is associated to a principal connection on an affine frame bundle 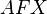 . In affine gauge theory, it is treated as an affine gauge field.
. In affine gauge theory, it is treated as an affine gauge field.
Given the linear bundle coordinates (1) on 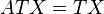 , an affine connection
, an affine connection  is represented by a connection tangent-valued form
is represented by a connection tangent-valued form
This affine connection defines a unique linear connection
on 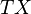 , which is associated to a principal connection on
, which is associated to a principal connection on 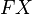 .
.
Conversely, every linear connection 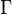 (4) on
(4) on 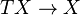 is extended to the affine one
is extended to the affine one 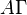 on
on 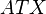 which is given by the same expression (4) as
which is given by the same expression (4) as 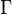 with respect to the bundle coordinates (1) on
with respect to the bundle coordinates (1) on 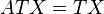 , but it takes a form
, but it takes a form
relative to the affine coordinates (2).
Then any affine connection  (3) on
(3) on 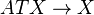 is represented by a sum
is represented by a sum
of the extended linear connection 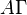 and a basic soldering form
and a basic soldering form
on 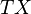 , where
, where 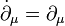 due to the canonical isomorphism
due to the canonical isomorphism 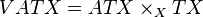 of the vertical tangent bundle
of the vertical tangent bundle 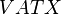 of
of 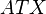 .
.
Relative to the linear coordinates (1), the sum (5) is brought into a sum 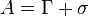 of a linear connection
of a linear connection 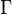 and the soldering form
and the soldering form  (6). In this case, the soldering form
(6). In this case, the soldering form  (6) often is treated as a translation gauge field, though it is not a connection.
(6) often is treated as a translation gauge field, though it is not a connection.
Let us note that a true translation gauge field (i.e., an affine connection which yields a flat linear connection on 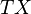 ) is well defined only on a parallelizable manifold
) is well defined only on a parallelizable manifold  .
.
Gauge theory of dislocations
In field theory, one meets a problem of physical interpretation of translation gauge fields because there are no fields subject to gauge translations 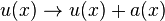 . At the same time, one observes such a field in gauge theory of dislocations in continuous media because, in the presence of dislocations, displacement vectors
. At the same time, one observes such a field in gauge theory of dislocations in continuous media because, in the presence of dislocations, displacement vectors 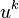 ,
, 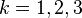 , of small deformations are determined only with accuracy to gauge translations
, of small deformations are determined only with accuracy to gauge translations 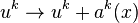 .
.
In this case, let 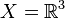 , and let an affine connection take a form
, and let an affine connection take a form
with respect to the affine bundle coordinates (2). This is a translation gauge field whose coefficients 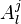 describe plastic distortion, covariant derivatives
describe plastic distortion, covariant derivatives 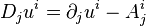 coincide with elastic distortion, and a strength
coincide with elastic distortion, and a strength 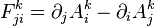 is a dislocation density.
is a dislocation density.
Equations of gauge theory of dislocations are derived from a gauge invariant Lagrangian density
where  and
and  are the Lamé parameters of isotropic media. These equations however are not independent since a displacement field
are the Lamé parameters of isotropic media. These equations however are not independent since a displacement field 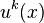 can be removed by gauge translations and, thereby, it fails to be a dynamic variable.
can be removed by gauge translations and, thereby, it fails to be a dynamic variable.
Gauge theory of the fifth force
In gauge gravitation theory on a world manifold  , one can consider an affine, but not linear connection on the tangent bundle
, one can consider an affine, but not linear connection on the tangent bundle 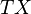 of
of  . Given bundle coordinates (1) on
. Given bundle coordinates (1) on 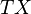 , it takes the form (3) where the linear connection
, it takes the form (3) where the linear connection 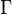 (4) and the basic soldering form
(4) and the basic soldering form  (6) are considered as independent variables.
(6) are considered as independent variables.
As was mentioned above, the soldering form  (6) often is treated as a translation gauge field, though it is not a connection. On another side, one mistakenly identifies
(6) often is treated as a translation gauge field, though it is not a connection. On another side, one mistakenly identifies  with a tetrad field. However, these are different mathematical object because a soldering form is a section of the tensor bundle
with a tetrad field. However, these are different mathematical object because a soldering form is a section of the tensor bundle 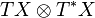 , whereas a tetrad field is a local section of a Lorentz reduced subbundle of a frame bundle
, whereas a tetrad field is a local section of a Lorentz reduced subbundle of a frame bundle 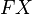 .
.
In the spirit of the above-mentioned gauge theory of dislocations, it has been suggested that a soldering field  can describe sui generi deformations of a world manifold
can describe sui generi deformations of a world manifold  which are given by a bundle morphism
which are given by a bundle morphism
where 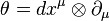 is a tautological one-form.
is a tautological one-form.
Then one considers metric-affine gravitation theory 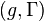 on a deformed world manifold as that with a deformed pseudo-Riemannian metric
on a deformed world manifold as that with a deformed pseudo-Riemannian metric 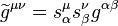 when a Lagrangian of a soldering field
when a Lagrangian of a soldering field  takes a form
takes a form
-
![L_{(\sigma)}=\frac12[a_1T^\mu{}_{\nu\mu} T_\alpha{}^{\nu\alpha}+
a_2T_{\mu\nu\alpha}T^{\mu\nu\alpha}+a_3T_{\mu\nu\alpha}T^{\nu\mu\alpha} +a_4\epsilon^{\mu\nu\alpha\beta}T^\gamma{}_{\mu\gamma}
T_{\beta\nu\alpha}-\mu\sigma^\mu{}_\nu\sigma^\nu{}_\mu+
\lambda\sigma^\mu{}_\mu \sigma^\nu{}_\nu]\sqrt{-g}](../I/m/013bbe1d1700bf15cea4a3d136510d06.png) ,
,
where 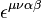 is the Levi-Civita symbol, and
is the Levi-Civita symbol, and
is the torsion of a linear connection 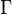 with respect to a soldering form
with respect to a soldering form  .
.
In particular, let us consider this gauge model in the case of small gravitational and soldering fields whose matter source is a point mass. Then one comes to a modified Newtonian potential of the fifth force type.
References
- A. Kadic, D. Edelen, A Gauge Theory of Dislocations and Disclinations, Lecture Notes in Physics 174 (Springer, New York, 1983), ISBN 3-540-11977-9
- G. Sardanashvily, O. Zakharov, Gauge Gravitation Theory (World Scientific, Singapore, 1992), ISBN 981-02-0799-9
- C. Malyshev, The dislocation stress functions from the double curl T(3)-gauge equations: Linearity and look beyond, Annals of Physics 286 (2000) 249.
External links
- G. Sardanashvily, Gravity as a Higgs field. III. Nongravitational deviations of gravitational field, arXiv: gr-qc/9411013.
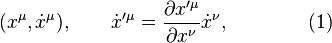
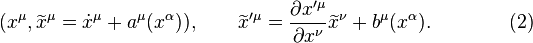
![A=dx^\lambda\otimes[\partial_\lambda + (\Gamma_\lambda{}^\mu{}_\nu(x^\alpha)\dot x^\nu+\sigma_\lambda^\mu(x^\alpha))\dot\partial_\mu].\qquad \qquad (3)](../I/m/563428a5b19ca7a26f112010489c276b.png)
![\Gamma =dx^\lambda\otimes[\partial_\lambda + \Gamma_\lambda{}^\mu{}_\nu(x^\alpha)\dot x^\nu\dot\partial_\mu] \qquad\qquad (4)](../I/m/3e1dac534170a9fb3051cc5c3d5b8b7c.png)
![A\Gamma =dx^\lambda\otimes[\partial_\lambda + (\Gamma_\lambda{}^\mu{}_\nu(x^\alpha)\widetilde x^\nu + s^\mu(x^\alpha))\widetilde\partial_\mu], \qquad s^\mu = - \Gamma_\lambda{}^\mu{}_\nu a^\nu +\partial_\lambda a^\mu,](../I/m/dc4bdd6c20501f39c6c55ee90e4c5332.png)