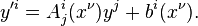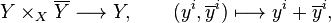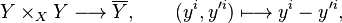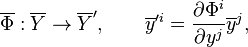Affine bundle
In mathematics, an affine bundle is a fiber bundle whose typical fiber, fibers, trivialization morphisms and transition functions are affine.[1]
Formal definition
Let 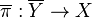 be a vector bundle with a typical fiber a vector space
be a vector bundle with a typical fiber a vector space 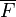 . An affine bundle modelled on a vector bundle
. An affine bundle modelled on a vector bundle 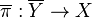 is a fiber bundle
is a fiber bundle 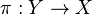 whose typical fiber
whose typical fiber 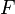 is an affine space modelled on
is an affine space modelled on 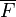 so that the following conditions hold:
so that the following conditions hold:
(i) All the fiber 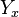 of
of  are affine spaces modelled over the corresponding fibers
are affine spaces modelled over the corresponding fibers 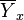 of a vector bundle
of a vector bundle 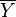 .
.
(ii) There is an affine bundle atlas of 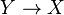 whose local trivializations morphisms and transition functions are affine isomorphisms.
whose local trivializations morphisms and transition functions are affine isomorphisms.
Dealing with affine bundles, one uses only affine bundle coordinates 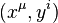 possessing affine transition functions
possessing affine transition functions
There are the bundle morphisms
where 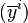 are linear bundle coordinates on a vector bundle
are linear bundle coordinates on a vector bundle 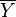 , possessing linear transition functions
, possessing linear transition functions 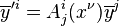 .
.
Properties
An affine bundle has a global section, but in contrast with vector bundles, there is no canonical global section of an affine bundle. Let 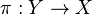 be an affine bundle modelled on a vector bundle
be an affine bundle modelled on a vector bundle 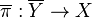 . Every global section
. Every global section  of an affine bundle
of an affine bundle 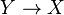 yields the bundle morphisms
yields the bundle morphisms
In particular, every vector bundle  has a natural structure of an affine bundle due to these morphisms where
has a natural structure of an affine bundle due to these morphisms where 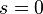 is the canonical zero-valued section of
is the canonical zero-valued section of  . For instance, the tangent bundle
. For instance, the tangent bundle 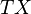 of a manifold
of a manifold  naturally is an affine bundle.
naturally is an affine bundle.
An affine bundle 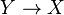 is a fiber bundle with a general affine structure group
is a fiber bundle with a general affine structure group 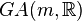 of affine transformations of its typical fiber
of affine transformations of its typical fiber  of dimension
of dimension  . This structure group always is reducible to a general linear group
. This structure group always is reducible to a general linear group 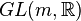 , i.e., an affine bundle admits an atlas with linear transition functions.
, i.e., an affine bundle admits an atlas with linear transition functions.
By a morphism of affine bundles is meant a bundle morphism 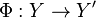 whose restriction to each fiber of
whose restriction to each fiber of  is an affine map. Every affine bundle morphism
is an affine map. Every affine bundle morphism 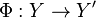 of an affine bundle
of an affine bundle  modelled on a vector bundle
modelled on a vector bundle 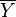 to an affine bundle
to an affine bundle  modelled on a vector bundle
modelled on a vector bundle 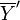 yields a unique linear bundle morphism
yields a unique linear bundle morphism
called the linear derivative of 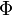 .
.
See also
Notes
- ↑ Kolář, Ivan; Michor, Peter; Slovák, Jan (1993), Natural operators in differential geometry (PDF), Springer-Verlag. (page 60)
References
- S. Kobayashi, K. Nomizu, Foundations of Differential Geometry, Vols. 1 & 2, Wiley-Interscience, 1996, ISBN 0-471-15733-3.
- Kolář, Ivan; Michor, Peter; Slovák, Jan (1993), Natural operators in differential geometry (PDF), Springer-Verlag
- Sardanashvily, G., Advanced Differential Geometry for Theoreticians. Fiber bundles, jet manifolds and Lagrangian theory, Lambert Academic Publishing, 2013, ISBN 978-3-659-37815-7; arXiv: 0908.1886.
- Saunders, D.J. (1989), The geometry of jet bundles, Cambridge University Press, ISBN 0-521-36948-7