Affine-regular polygon
In geometry, an affine-regular polygon or affinely regular polygon is a polygon that is related to a regular polygon by an affine transformation. Affine transformations include translations, uniform and non-uniform scaling, reflections, rotations, shears, and other similarities and some, but not all linear maps.
All triangles are affine-regular. In other words, all triangles can be generated by applying affine transformations to an equilateral triangle. A quadrilateral is affine-regular if and only if it is a parallelogram, which includes rectangles and rhombuses as well as squares. In fact, affine-regular polygons may be considered a natural generalization of parallelograms.[1]
Many properties of regular polygons are invariant under affine transformations, and affine-regular polygons share the same properties. For instance,
an affine-regular quadrilateral can be equidissected into  equal-area triangles if and only if
equal-area triangles if and only if  is even, by affine invariance of equidissection and Monsky's theorem on equidissections of squares.[2] More generally an
is even, by affine invariance of equidissection and Monsky's theorem on equidissections of squares.[2] More generally an  -gon with
-gon with 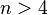 may be equidissected into
may be equidissected into  equal-area triangles if and only if
equal-area triangles if and only if  is a multiple of
is a multiple of  .[3]
.[3]
References
- ↑ Coxeter, H. S. M. (December 1992), "Affine regularity", Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg 62 (1): 249–253, doi:10.1007/BF02941630. See in particular p. 249.
- ↑ Monsky, P. (1970), "On Dividing a Square into Triangles", The American Mathematical Monthly 77 (2): 161–164, doi:10.2307/2317329, MR 0252233.
- ↑ Kasimatis, Elaine A. (December 1989), "Dissections of regular polygons into triangles of equal areas", Discrete & Computational Geometry 4 (1): 375–381, doi:10.1007/BF02187738, Zbl 0675.52005.