Adaptive control

Adaptive control is the control method used by a controller which must adapt to a controlled system with parameters which vary, or are initially uncertain. For example, as an aircraft flies, its mass will slowly decrease as a result of fuel consumption; a control law is needed that adapts itself to such changing conditions. Adaptive control is different from robust control in that it does not need a priori information about the bounds on these uncertain or time-varying parameters; robust control guarantees that if the changes are within given bounds the control law need not be changed, while adaptive control is concerned with control law changing themselves.

Parameter estimation

The foundation of adaptive control is parameter estimation. Common methods of estimation include recursive least squares and gradient descent. Both of these methods provide update laws which are used to modify estimates in real time (i.e., as the system operates). Lyapunov stability is used to derive these update laws and show convergence criterion (typically persistent excitation). Projection (mathematics) and normalization are commonly used to improve the robustness of estimation algorithms. It is also called adjustable control.

Classification of adaptive control techniques

In general one should distinguish between:

1. Feedforward Adaptive Control
2. Feedback Adaptive Control

as well as between

1. Direct Methods and
2. Indirect Methods

Direct methods are ones wherein the estimated parameters are those directly used in the adaptive controller. In contrast, indirect methods are those in which the estimated parameters are used to calculate required controller parameters^[1]

There are several broad categories of feedback adaptive control (classification can vary):

• Dual Adaptive Controllers [based on Dual control theory]
  • Optimal Dual Controllers [difficult to design]
  • Suboptimal Dual Controllers
• Nondual Adaptive Controllers
  • Adaptive Pole Placement
  • Extremum Seeking Controllers
  • Iterative learning control
  • Gain scheduling
  • Model Reference Adaptive Controllers (MRACs) [incorporate a reference model defining desired closed loop performance]
    

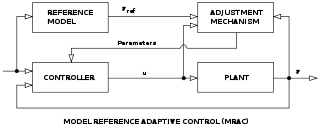    MRAC
    

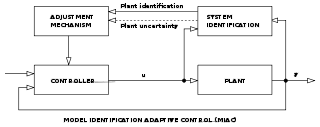    MIAC
    • Gradient Optimization MRACs [use local rule for adjusting params when performance differs from reference. Ex.: "MIT rule".]
    • Stability Optimized MRACs
  • Model Identification Adaptive Controllers (MIACs) [perform System identification while the system is running]
    • Cautious Adaptive Controllers [use current SI to modify control law, allowing for SI uncertainty]
    • Certainty Equivalent Adaptive Controllers [take current SI to be the true system, assume no uncertainty]
      • Nonparametric Adaptive Controllers
      • Parametric Adaptive Controllers
        • Explicit Parameter Adaptive Controllers
        • Implicit Parameter Adaptive Controllers

Some special topics in adaptive control can be introduced as well:

1. Adaptive Control Based on Discrete-Time Process Identification
2. Adaptive Control Based on the Model Reference Technique
3. Adaptive Control based on Continuous-Time Process Models
4. Adaptive Control of Multivariable Processes
5. Adaptive Control of Nonlinear Processes

Applications

When designing adaptive control systems, special consideration is necessary of convergence and robustness issues. Lyapunov stability is typically used to derive control adaptation laws and show convergence.

Typical applications of adaptive control are (in general):

• Self-tuning of subsequently fixed linear controllers during the implementation phase for one operating point;
• Self-tuning of subsequently fixed robust controllers during the implementation phase for whole range of operating points;
• Self-tuning of fixed controllers on request if the process behaviour changes due to ageing, drift, wear etc.;
• Adaptive control of linear controllers for nonlinear or time-varying processes;
• Adaptive control or self-tuning control of nonlinear controllers for nonlinear processes;
• Adaptive control or self-tuning control of multivariable controllers for multivariable processes (MIMO systems);

Usually these methods adapt the controllers to both the process statics and dynamics. In special cases the adaptation can be limited to the static behavior alone, leading to adaptive control based on characteristic curves for the steady-states or to extremum value control, optimizing the steady state. Hence, there are several ways to apply adaptive control algorithms.

See also

• Nonlinear control
• Intelligent control
• Lyapunov optimization

References

Further reading

• B. Egardt, Stability of Adaptive Controllers. New York: Springer-Verlag, 1979.
• I. D. Landau, Adaptive Control: The Model Reference Approach. New York: Marcel Dekker, 1979.
• P. A. Ioannou and J. Sun, Robust Adaptive Control. Upper Saddle River, NJ: Prentice-Hall, 1996.
• K. S. Narendra and A. M. Annaswamy, Stable Adaptive Systems. Englewood Cliffs, NJ: Prentice Hall, 1989; Dover Publications, 2004.
• S. Sastry and M. Bodson, Adaptive Control: Stability, Convergence and Robustness. Prentice Hall, 1989.
• K. J. Astrom and B. Wittenmark, Adaptive Control. Reading, MA: Addison-Wesley, 1995.
• I. D. Landau, R. Lozano, and M. M’Saad, Adaptive Control. New York, NY: Springer-Verlag, 1998.
• G. Tao, Adaptive Control Design and Analysis. Hoboken, NJ: Wiley-Interscience, 2003.
• P. A. Ioannou and B. Fidan, Adaptive Control Tutorial. SIAM, 2006.
• G. C. Goodwin and K. S. Sin, Adaptive Filtering Prediction and Control. Englewood Cliffs, NJ: Prentice-Hall, 1984.
• M. Krstic, I. Kanellakopoulos, and P. V. Kokotovic, Nonlinear and Adaptive Control Design. Wiley Interscience, 1995.
• P. A. Ioannou and P. V. Kokotovic, Adaptive Systems with Reduced Models. Springer Verlag, 1983.

External links

• Shankar Sastry and Marc Bodson, Adaptive Control: Stability, Convergence, and Robustness, Prentice-Hall, 1989-1994 (book)
• K. Sevcik: Tutorial on Model Reference Adaptive Control (Drexel University)