Adam7 algorithm


Adam7 is an interlacing algorithm for raster images, best known as the interlacing scheme optionally used in PNG images. An Adam7 interlaced image is broken into seven subimages, which are defined by replicating this 8×8 pattern across the full image.
1 6 4 6 2 6 4 6 7 7 7 7 7 7 7 7 5 6 5 6 5 6 5 6 7 7 7 7 7 7 7 7 3 6 4 6 3 6 4 6 7 7 7 7 7 7 7 7 5 6 5 6 5 6 5 6 7 7 7 7 7 7 7 7 |
The subimages are then stored in the image file in numerical order.
Adam7 uses seven passes and operates in both dimensions, compared to only four passes in the vertical dimension used by GIF. This means that an approximation of the entire image can be perceived much more quickly in the early passes, particularly if interpolation algorithms such as bicubic interpolation are used.[1]
History
Adam7 is named after Adam M. Costello, who suggested the method on January 30, 1995, based on this five-pass scheme that had earlier been proposed by Lee Daniel Crocker:[2]
1 4 2 4 5 5 5 5 3 4 3 4 5 5 5 5 |
Alternative speculative proposals at the time included square spiral interlacing and using Peano curves, but these were rejected as being overly complicated.
Passes
The pixels included in each pass, and the total pixels encoded at that point are as follows:
-

Pass 1, 1/64 = 1.5625%
-

Pass 2, 1/32 = 3.125%
-
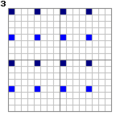
Pass 3, 1/16 = 6.25%
-

Pass 4, 1/8 = 12.5%
-

Pass 5, 1/4 = 25%
-

Pass 6, 1/2 = 50%
-

Pass 7, 1/1 = 100%
When rendering, the image will generally be interpolated at earlier stages, rather than just these pixels being rendered.
Related algorithms
Adam7 is a multiscale model of the data, similar to a discrete wavelet transform with Haar wavelets, though it starts from an 8×8 block, and downsamples the image, rather than decimating (low-pass filtering, then downsampling). It thus offers worse frequency behavior, showing artifacts (pixelation) at the early stages, in return for simpler implementation.
Iteration
Adam7 arises from iteration of the following pattern:
12 33 |
which may be interpreted as "folding" in the vertical and horizontal dimensions. Similarly, GIF interlacing 1324 can be seen as iteration of the 12 pattern, but only in the vertical direction (12 expands to 1.2. which is filled in as 1324).
Using this 3-pass pattern means the first pass is (1/2)2 = 1/4 (25%) of the image.
Iterating this pattern once yields Crocker's 5-pass scheme; after 3 passes this yields
1 . 2 . . . . . 3 . 3 . . . . . |
which is then filled in to:
1 4 2 4 5 5 5 5 3 4 3 4 5 5 5 5 |
In the 5-pass pattern, the first pass (1/4)2 = 1/16 (6.25%) of the image.
Iterating again yields the 7-pass Adam7 scheme, where the first pass (1/8)2 = 1/64 (1.5625%) of the image.
In principle this can be iterated, yielding a 9-pass scheme, an 11-pass scheme, and so forth, or alternatively an adaptive number of passes can be used, as many as the image size will allow (so the first pass consists of a single pixel), as is usual in scale-free multiscale modeling. In the context that PNG was developed (i.e., for the image sizes and connection speeds in question), a 7-pass scheme was seen as sufficient, and preferable to a simple 5-pass scheme.
References
- ↑ Introduction to PNG - nuwen.net
- ↑ Costello, Adam M. (30 Jan 1995). "Re: CRC". png-list (Mailing list). Retrieved 2010-01-29.
By the way, what would folks think of a Lee-style 7-pass scheme? Just the same thing, but starting with a 1/64 image? That would make the initial large pixels 8x8.