Acnode

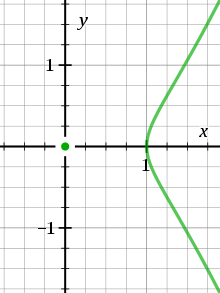
An acnode at the origin (curve described in text)

An acnode is an isolated point not on a curve, but whose coordinates satisfy the equation of the curve. The term "isolated point" or "hermit point" is an equivalent term.^[1]

Acnodes are commonly found in the study of algebraic curves over fields which are not algebraically closed, defined as the zero set of a polynomial of two variables. For example the equation

f(x,y)=y^2+x^2-x^3=0\;

has an acnode at the origin of 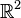$\mathbb{R}^2$ , because it is equivalent to

y^2 = x^2 (x-1)

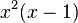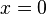and $x^2(x-1)$ is non-negative when $x$ ≥ 1 and when $x = 0$ . Thus, over the real numbers the equation has no solutions for 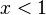$x < 1$ except for (0, 0).

In contrast, over the complex numbers the origin is not isolated since square roots of negative real numbers exist.

An acnode is a singularity of the function, where both partial derivatives 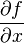$\partial f\over \partial x$ and $\partial f\over \partial y$ vanish. Further the Hessian matrix of second derivatives will be positive definite or negative definite. Hence the function has a local minimum or a local maximum.

References

↑ Hazewinkel, M. (2001), "Acnode", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4

Porteous, Ian (1994). Geometric Differentation. Cambridge University Press. ISBN 0-521-39063-X.

Topics in algebraic curves

Rational curves

Elliptic curves

Analytic theory	Elliptic function Elliptic integral Fundamental pair of periods Modular form

Arithmetic theory	Counting points on elliptic curves Division polynomials Hasse's theorem on elliptic curves Mazur's torsion theorem Modular elliptic curve Modularity theorem Mordell–Weil theorem Nagell–Lutz theorem Supersingular elliptic curve Schoof's algorithm Schoof–Elkies–Atkin algorithm

Applications	Elliptic curve cryptography Elliptic curve primality

Higher genus

Plane curves

Riemann surfaces

Constructions

Structure of curves

Divisors on curves	Abel–Jacobi map Brill–Noether theory Clifford's theorem on special divisors Gonality of an algebraic curve Jacobian variety Riemann–Roch theorem Weierstrass point Weil reciprocity law

Moduli	ELSV formula Gromov–Witten invariant Hodge bundle Moduli of algebraic curves Stable curve

Morphisms	Hasse–Witt matrix Riemann–Hurwitz formula Prym variety Weber's theorem

Singularities	Acnode Crunode Cusp Delta invariant Tacnode

Vector bundles	Birkhoff–Grothendieck theorem Stable vector bundle Vector bundles on algebraic curves

Acnode

See also

References