Accessible category
The theory of accessible categories originates from the work of Grothendieck completed by 1969 (Grothendieck (1972)) and Gabriel-Ulmer (1971). It has been further developed in 1989 by Michael Makkai and Robert Paré, with motivation coming from model theory, a branch of mathematical logic.[1] Accessible categories have also applications in homotopy theory.[1][2] Grothendieck also continued the development of the theory for homotopy-theoretic purposes in his (still partly unpublished) 1991 manuscript Les dérivateurs (Grothendieck (1991)). Some properties of accessible categories depend on the set universe in use, particularly on the cardinal properties.[3]
Definition
Let 
be an infinite regular cardinal and let 
be a category.
An object 
of is called -presentable if the Hom functor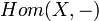 
preserves -directed colimits.
The category is called -accessible provided that :
- has -directed colimits
- has a set
of -presentable objects such that every object of is a -directed colimit of objects of
A category is called accessible if is -accessible for some infinite regular cardinal .
A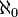 
-presentable object is usually called finitely presentable, and
an 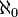-accessible category is often called finitely accessible.
Examples
- The category
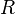of (left) 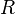-modules is finitely accessible for any ring 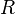. The objects that are finitely presentable in the above sense are precisely the finitely presented modules (which are not necessarily the same as the finitely generated modules unless 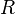is noetherian). - The category of simplicial sets is finitely-accessible.
- The category Mod(T) of models of some first-order theory T with countable signature is
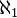-accessible. 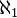-presentable objects are models with a countable number of elements.
Further notions
When the category is cocomplete, is called a locally presentable category.
Locally presentable categories are also complete.
References
- ↑ 1.0 1.1 J. Rosicky "On combinatorial model categories", Arxiv, 16 August 2007. Retrieved on 19 January 2008.
- ↑ J. Rosicky, Injectivity and accessible categories
- ↑ J. Adamek and J. Rosicky, Locally Presentable and Accessible Categories, Cambridge University Press 1994
Further reading
- Adámek, Jiří; Rosicky, Jiří (1994), Locally presentable and accessible categories, LNM Lecture Notes, CUP, ISBN 0-521-42261-2
- Gabriel, P; Ulmer, F (1971), Lokal Präsentierbare Kategorien, Lecture Notes in Mathematics 221, Springer
- Grothendieck, Alexander et al. (1972), Théorie des Topos et Cohomologie Étale des Schémas, Lecture Notes in Mathematics 269, Springer
- Grothendieck, Alexander (1991), Les dérivateurs, Contemporary Mathematics, manuscript (Les Dérivateurs: Texte d'Alexandre Grothendieck. Édité par M. Künzer, J. Malgoire, G. Maltsiniotis)
- Makkai, Michael; Paré, Robert (1989), Accessible categories: The foundation of Categorical Model Theory, Contemporary Mathematics, AMS, ISBN 0-8218-5111-X