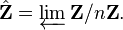Absolute Galois group

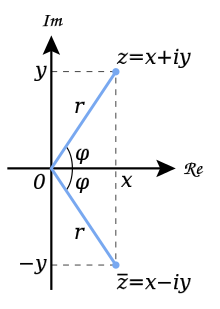
The absolute Galois group of the real numbers is a cyclic group of order 2 generated by complex conjugation, since C is the separable closure of R and [C:R] = 2.

In mathematics, the absolute Galois group G_K of a field K is the Galois group of K^sep over K, where K^sep is a separable closure of K. Alternatively it is the group of all automorphisms of the algebraic closure of K that fix K. The absolute Galois group is unique up to isomorphism. It is a profinite group.

(When K is a perfect field, K^sep is the same as an algebraic closure K^alg of K. This holds e.g. for K of characteristic zero, or K a finite field.)

Examples

• The absolute Galois group of an algebraically closed field is trivial.
• The absolute Galois group of the real numbers is a cyclic group of two elements (complex conjugation and the identity map), since C is the separable closure of R and [C:R] = 2.
• The absolute Galois group of a finite field K is isomorphic to the group

(For the notation, see Inverse limit.)

The Frobenius automorphism Fr is a canonical (topological) generator of G_K. (Recall that Fr(x) = x^q for all x in K^alg, where q is the number of elements in K.)

• The absolute Galois group of the field of rational functions with complex coefficients is free (as a profinite group). This result is due to Adrien Douady and has its origins in Riemann's existence theorem.^[1]
• More generally, let C be an algebraically closed field and x a variable. Then the absolute Galois group of K = C(x) is free of rank equal to the cardinality of C. This result is due to David Harbater and Florian Pop, and was also proved later by Dan Haran and Moshe Jarden using algebraic methods.^[2][3][4]
• Let K be a finite extension of the p-adic numbers Q_p. For p ≠ 2, its absolute Galois group is generated by [K:Q_p] + 3 elements and has an explicit description by generators and relations. This is a result of Uwe Jannsen and Kay Wingberg.^[5][6] Some results are known in the case p = 2, but the structure for Q₂ is not known.^[7]
• Another case in which the absolute Galois group has been determined is for the largest totally real subfield of the field of algebraic numbers.^[8]

Problems

• No direct description is known for the absolute Galois group of the rational numbers. In this case, it follows from Belyi's theorem that the absolute Galois group has a faithful action on the dessins d'enfants of Grothendieck (maps on surfaces), enabling us to "see" the Galois theory of algebraic number fields.

• Let K be the maximal abelian extension of the rational numbers. Then Shafarevich's conjecture asserts that the absolute Galois group of K is a free profinite group.^[9]

Some general results

• Every profinite group occurs as a Galois group of some Galois extension,^[10] however not every profinite group occurs as an absolute Galois group. For example, the Artin–Schreier theorem asserts that the only finite absolute Galois groups are the trivial one and the cyclic group of order 2.

• Every projective profinite group can be realized as an absolute Galois group of a pseudo algebraically closed field. This result is due to Alexander Lubotzky and Lou van den Dries.^[11]

Notes

References

• Douady, Adrien (1964), "Détermination d'un groupe de Galois", Comptes Rendues de l'Académie des Sciences de Paris 258: 5305–5308, MR 0162796 
• Fried, Michael D.; Jarden, Moshe (2008), Field arithmetic, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge 11 (3rd ed.), Springer-Verlag, ISBN 978-3-540-77269-9, Zbl 1145.12001 
• Haran, Dan; Jarden, Moshe (2000), "The absolute Galois group of C(x)", Pacific Journal of Mathematics 196 (2): 445–459, doi:10.2140/pjm.2000.196.445, MR 1800587 
• Harbater, David, "Fundamental groups and embedding problems in characteristic p", Recent developments in the inverse Galois problem, Contemporary Mathematics 186, Providence, RI: American Mathematical Society, pp. 353–369, MR 1352282 
• Jannsen, Uwe; Wingberg, Kay (1982), "Die Struktur der absoluten Galoisgruppe 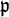-adischer Zahlkörper", Inventiones Mathematicae 70: 71–78, doi:10.1007/bf01393199 
• Neukirch, Jürgen; Schmidt, Alexander; Wingberg, Kay (2000), Cohomology of Number Fields, Grundlehren der Mathematischen Wissenschaften 323, Berlin: Springer-Verlag, ISBN 978-3-540-66671-4, Zbl 0948.11001, MR 1737196 
• Pop, Florian (1995), "Étale Galois covers of affine smooth curves. The geometric case of a conjecture of Shafarevich. On Abhyankar's conjecture", Inventiones Mathematicae 120 (3): 555–578, doi:10.1007/bf01241142, MR 1334484