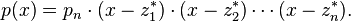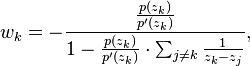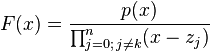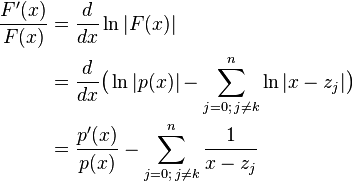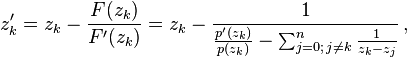Aberth method

The Aberth method, or Aberth–Ehrlich method, named after Oliver Aberth[1] and Louis W. Ehrlich,[2] is a root-finding algorithm for simultaneous approximation of all the roots of a univariate polynomial.

The fundamental theorem of algebra states that for each polynomial with complex coefficients there are as many roots as the degree of the polynomial. Numerical algorithms that approximate all roots at once include the Weierstrass–(Durand–Kerner) method and the Aberth–Ehrlich method.

Description

Let 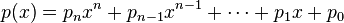p(x)=p_nx^n+p_{n-1}x^{n-1}+\cdots+p_1x+p_0 be a univariate polynomial of degree n with real or complex coefficients. Then there exist complex numbers 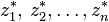z^*_1,\,z^*_2,\dots,z^*_n, the roots of p(x), that give the factorisation:

p(x)=p_n\cdot(x-z^*_1)\cdot(x-z^*_2)\cdots(x-z^*_n).

Although those numbers are unknown, upper and lower bounds for their absolute values are computable from the coefficients of the polynomial. Now one can pick n distinct numbers in the complex plane—randomly or evenly distributed—such that their absolute values are within the same bounds. A set of such numbers is called an initial approximation of the set of roots of p(x). This approximation can be iteratively improved using the following procedure.

Let 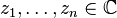z_1,\dots,z_n\in\mathbb C be the current approximations of the zeros of p(x). Then offset numbers 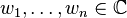w_1,\dots,w_n\in\mathbb C are computed as

w_k=-\frac{\frac{p(z_k)}{p'(z_k)}}{1-\frac{p(z_k)}{p'(z_k)}\cdot \sum_{j\ne k}\frac1{z_k-z_j}},

where p'(z) is the polynomial derivative of p evaluated in the point z.

The next set of approximations of roots of p(x) is then 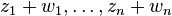z_1+w_1,\dots,z_n+w_n . One can measure the quality of the current approximation by the values of the polynomial or by the size of the offsets.

Inside the formula of the Aberth method one can find elements of Newton's method and the Weierstrass–(Durand–Kerner) method. Details for an efficient implementation, esp. on the choice of good initial approximations, can be found in Bini (1996).[3]

Derivation from Newton's method

The iteration formula is the univariate Newton iteration for the function

F(x)=\frac{p(x)}{\prod_{j=0;\,j\ne k}^n(x-z_j)}

If the values 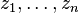z_1,\dots,z_n are already close to the roots of p(x), then the rational function F(x) is almost linear with a dominant root close to 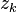z_k and poles at 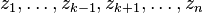z_1,\dots,z_{k-1},z_{k+1},\dots,z_n that direct the Newton iteration away from the roots of p(x) that are close to them. That is, the corresponding basins of attraction get rather small, while the root close to 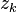z_k has a wide region of attraction.

The Newton step 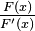\tfrac{F(x)}{F'(x)} in the univariate case is the reciprocal value to the logarithmic derivative

\begin{align} \frac{F'(x)}{F(x)} &= \frac{d}{dx}\ln|F(x)|\\ &= \frac{d}{dx}\big(\ln|p(x)|-\sum_{j=0;\,j\ne k}^n\ln|x-z_j|\big)\\ &= \frac{p'(x)}{p(x)}-\sum_{j=0;\,j\ne k}^n\frac1{x-z_j} \end{align}

Thus, the new approximation is computed as

z_k'=z_k-\frac{F(z_k)}{F'(z_k)}=z_k-\frac1{\frac{p'(z_k)}{p(z_k)}-\sum_{j=0;\,j\ne k}^n\frac1{z_k-z_j}}\,,

which is the update formula of the Aberth–Ehrlich method.

The updates of the roots may be executed as a simultaneous Jacobi-like iteration where first all new approximations are computed from the old approximations or as a sequential Gauss–Seidel-like iteration that uses each new approximation from the time it is computed.

Literature

  1. ↑ Aberth, Oliver (1973). "Iteration methods for finding all zeros of a polynomial simultaneously". Math. Comp. (Mathematics of Computation, Vol. 27, No. 122) 27 (122): 339–344. doi:10.2307/2005621. JSTOR 2005621.
  2. ↑ Ehrlich, Louis W. (1967). "A modified Newton method for polynomials". Comm. ACM 10 (2): 107–108. doi:10.1145/363067.363115.
  3. ↑ Bini, Dario Andrea (1996). "Numerical computation of polynomial zeros by means of Aberth's method". Numerical Algorithms 13 (2): 179–200. doi:10.1007/BF02207694.

See also