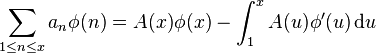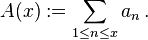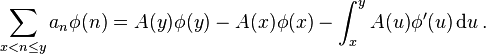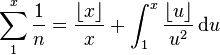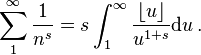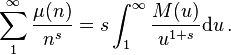Abel's summation formula

Another concept sometimes known by this name is summation by parts.

In mathematics, Abel's summation formula, introduced by Niels Henrik Abel, is intensively used in number theory to compute series.

Identity

Let 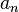a_n \, be a sequence of real or complex numbers and 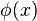\phi (x) \, a function of class 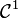\mathcal{C}^1 \,. Then

\sum_{1 \le n \le x} a_n \phi(n) = A(x)\phi(x) - \int_1^x A(u)\phi'(u) \, \mathrm{d}u \,

where

A(x):= \sum_{1 \le n \le x} a_n \,.

Indeed, this is integration by parts for a Riemann–Stieltjes integral.

More generally, we have

\sum_{x< n\le y} a_n\phi(n) = A(y)\phi(y) - A(x)\phi(x) -\int_x^y A(u)\phi'(u)\,\mathrm{d}u \,.

Examples

Euler–Mascheroni constant

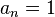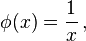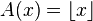If a_n = 1 \, and \phi (x) = \frac{1}{x} \,, then A (x) = \lfloor x \rfloor \, and

\sum_1^x \frac{1}{n} = \frac{\lfloor x \rfloor}{x} + \int_1^x \frac{\lfloor u \rfloor}{u^2} \, \mathrm{d}u

which is a method to represent the Euler–Mascheroni constant.

Representation of Riemann's zeta function

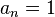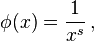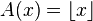If a_n = 1 \, and \phi (x) = \frac{1}{x^s} \,, then A (x) = \lfloor x \rfloor \, and

\sum_1^\infty \frac{1}{n^s} = s\int_1^\infty \frac{\lfloor u\rfloor}{u^{1+s}} \mathrm{d}u \,.

The formula holds for 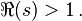\Re(s) > 1 \,. It may be used to derive Dirichlet's theorem, that is, 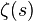\zeta(s) \, has a simple pole with residue 1 in s = 1.

Reciprocal of Riemann zeta function

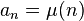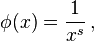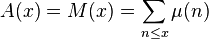If a_n = \mu (n) \, is the Möbius function and \phi (x) = \frac{1}{x^s} \,, then A (x) = M(x) = \sum_{n \le x} \mu (n) \, is Mertens function and

\sum_1^\infty \frac{\mu(n)}{n^s} = s \int_1^\infty \frac{M(u)}{u^{1+s}} \mathrm{d}u \,.

This formula holds for 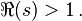\Re(s) > 1 \,.

See also

References